已實行在使用長纖維複合物材料執行纖維配向分析時計算纖維斷裂的選項。
所實行的纖維斷裂模型最早由 Phelps 與 Tucker [1] 作為統計模型提出，其中描述因流場中的挫曲與剪應力導致纖維斷裂的可能性。
針對單一纖維，在流體動力下斷裂的可能性可表示為：
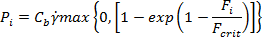
其中力比率為相對於臨界挫曲力的流體動力壓縮力，由 Dinh 與 Armstrong 描述[2]，例如：
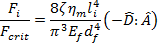
其中，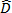 
與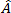 
分別爲為變形率張量與纖維配向張量。其他變數為纖維與母體的性質，除了 
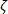，它是拖曳係數。
無論纖維是否斷裂，都必須遵循保守定律，因為纖維既無法消失，也無法在流場中增長。此保守定律可表示為：
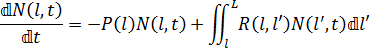
其中 L 是初始纖維長度，N(l,t) 是於時間 t 時長度為 l 的纖維數，P(l) 是纖維長度 l 的純量可能性函數，R(l,l') 是纖維長度 l 斷裂以形成長度 l' 之纖維的可能性函數 (其中 l'<l)。其可表示為高斯斷裂曲線，例如：
其中，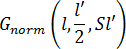 
是平均值為 l'/2 且標準偏差為 Sl' 之變數 l 的高斯正態概率密度函數。S 是無尺寸的調適參數，可用來控制高斯斷裂曲線的形狀。
參考文獻
- Phelps, J.H., Processing-microstructure Models for Short- and Long-fiber Thermoplastic Composites。Ph.D. thesis, University of Illinois at Urbana-Champaign (2009).
- Dinh, S.M. and Armstrong, R.C., A Rheological Equation of State for Semi-Concentrated Fiber Suspensions. J. Rheol., 28(3):207-227 (1984).