在模具充填期間對三維纖維配向進行數字預測,是以針對流體懸浮液中剛體微粒使用的運動方程式為基礎。
分析包含兩個可識別的項:
- 流體動力項。
- 互動項。
對微粒運動產生的流體動力影響由 Jeffery 假設無限縱橫比的方程式描述。此理論嚴格適用於稀釋懸浮液,但已顯示提供定性上與實驗資料一致的實用結果。
互動項由 Folgar 與 Tucker 提出,已用於為纖維間的機械互動隨機影響塑型。其形式為擴散項,互動頻率與應變率大小成比例。互動項的影響是要減少 Jeffery 的模型針對某些流條件預測的高度對齊配向狀態,改善了與實驗觀察之間的一致性。
纖維配向的定義與預測
對相同有限元素網格的三維纖維配向計算會與模具充填分析同時執行。會將每一個三角形元素視為由數個細分局部成型厚度的圖層組成。每一個圖層都由圖層通過的網格點識別。成型品的中間平面會通過網格點 1。會針對網格中的每個元素計算每個圖層上的配向解。如此便可以在一組平行於模具表面 (穿過成型品剖面) 的平面上觀察配向分佈的變化。
每個元素的三維配向解皆由二級張量描述。會針對圖形表現法產生配向張量的特徵值與特徵向量。特徵向量指示纖維對齊的主方向,特徵值則提供纖維相對這些方向對齊的統計比例 (0 至 1)。此資訊可用於定義配向橢球,其可完整描述每一個元素的纖維對齊分佈。下圖展示一般配向橢球。
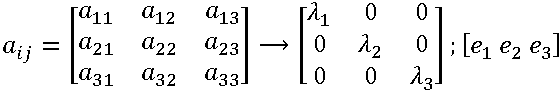
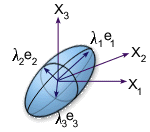
針對顯示的目的,這個 3D 橢球會投影到每個元素的平面上,以產生平面橢球。這會為配向分佈建立實用的表現法,因為由投影消除的塑件厚度方向配向分量通常很小。在此表現法中,有一個幾近隨機的分佈顯示為接近圓形的橢圓,而對於高度對齊的分佈,橢圓會退化為線。
配向張量的描述
二級配向張量 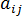 為射出成型中的纖維配向提供有效的描述。張量有九個分量,且張量項的下標為:
為射出成型中的纖維配向提供有效的描述。張量有九個分量,且張量項的下標為:
- 流動方向。
- 流動方向的橫向。
- 厚度方向。
通常適用於這些軸:
- X-Y (或 1-2) 流平面。
- 厚度方向的 Z 軸,位於 1-2 流平面之外。
由於以下原因,原始的九個分量會減少至五個獨立分量:
- 張量對稱性
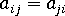 ,和
,和 - 正規化條件
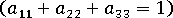
這三個主配向分量已包含在配向考量因素之中:
-
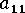 ,流動方向的纖維配向,從 0 到 1.0 不等。
,流動方向的纖維配向,從 0 到 1.0 不等。 -
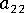 ,橫向於流的纖維配向,從 0 到 1.0 不等。
,橫向於流的纖維配向,從 0 到 1.0 不等。 -
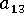 ,1-3 平面中的配向傾斜,從 -0.5 到 0.5 不等。
,1-3 平面中的配向傾斜,從 -0.5 到 0.5 不等。
注意事項:流動方向配向項 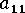 中包含有關微結構的大部分定量資訊,對流、製程和材料變化最為敏感。
中包含有關微結構的大部分定量資訊,對流、製程和材料變化最為敏感。
纖維配向模型
可能會將感興趣的複合材料視為黏性媒介中懸浮的顆粒或纖維。纖維之間可能會有機械與/或流體動力互動。
懸浮液可能為稀釋、半濃縮或濃縮,如以下討論:
-
稀釋懸浮液中的纖維彼此之間永遠不會靠近也不會互動。
-
半濃縮懸浮液中的纖維之間沒有機械接觸,但流體動力互動會變得很明顯。
-
在濃縮懸浮液中,纖維配向行為會變得非常複雜,因為機械與流體動力纖維互動都適用。
Jeffery 先為浸泡在大量不可壓縮牛頓流體中的單一纖維運動塑型。Jeffery 的模型僅適用於已稀釋到任何纖維間互動 (甚至是流體動力互動) 都會被忽略不計的懸浮液。
若要評估懸浮液濃縮程度,有一個重要的方法,就是平均分佈纖維之間的距離。
對於直徑為 (d)、長度為 (L) 的纖維,縱橫比為 (L/d),按體積的纖維濃度為 (c) (或體積分率 ) 且具有均勻的長度分佈,典型濃度分類等級為:
- 稀釋c << (d/L)2。
- 半濃縮 (d/L)2 < c < (d/L)。
- 濃縮 c > d/L。
例如,如果 L/d 為 10 (對於複合物中的強化纖維而言屬於較小值),若要使用 Jeffery 的方程式,按體積的纖維濃度必須小於 1%。
對於商用材料,纖維縱橫比 L/d 通常為 20 或以上,因此針對上述濃度的值為:
- 稀釋,c << 0.025。
- 半濃縮,0.0025 < c < 0.05。
- 濃縮,c > 0.05
這些分類等級臨界值通常可轉換為按重量的約 0.5% 及 10%。
多數商業複合材料中都包含佔重量 10% 至 50% 的纖維,可將其視為濃縮懸浮液。
Dinh 與 Armstrong 針對半濃縮懸浮液提出了一個模型。纖維的配向依循流體的整體變形,但微粒無法拉伸。
對於濃縮懸浮液,又稱為「互動係數」(或  ) 的項,已納入由 Folgar 與 Tucker 所提出的纖維配向現象模型中:
) 的項,已納入由 Folgar 與 Tucker 所提出的纖維配向現象模型中:
- 纖維間的互動傾向於隨機配向。
- 此項採取與擴散項相同的形式,且由於互動只在懸浮液變形時發生,有效擴散會與應變率成比例。
- 無尺寸的
 項決定了擴散項的強度。
項決定了擴散項的強度。
加入旋轉擴散項以說明纖維互動,已發現可改善配向預測,因為 Jeffery 的方程式本身並沒有為纖維配向提供質的預測準確性。
到目前為止,Folgar-Tucker 模型已是在濃縮懸浮液中為纖維配向塑型最好的模型。Advani 與 Tucker 以此形式提供模型:
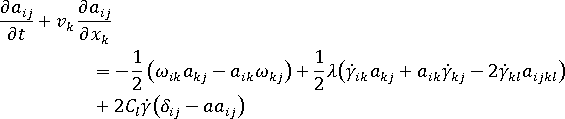
其中:
-
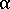 在 3D 配向下等於 3,在平面 (2D) 配向下等於 2
在 3D 配向下等於 3,在平面 (2D) 配向下等於 2 -
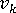 是速度分量
是速度分量 -
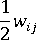 是旋度張量,
是旋度張量,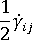 是變形率張量。
是變形率張量。 -
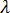 是取決於微粒幾何圖形的常數
是取決於微粒幾何圖形的常數 -
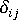 是單位張量
是單位張量 -
 是互動係數
是互動係數
纖維配向模型閉合
Advani 與 Tucker 的纖維配向模型的張量形式並非二級配向張量的適當導數,因為它包含了四級張量 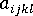 。
。
四級張量的導數包含六級配向張量,依此類推。展開適當導數的唯一方法是在二級張量方面逼近四級張量。
此逼近稱為"「閉合逼近」。"Advani 與 Tucker 已對各種逼近進行測試。但是,逼近本身的存在可能會引發模擬結果發生錯誤。因此閉合逼近是此模型最棘手的問題。 的任何值 都無法使纖維配向模型運算式符合所有配向模型元件。
的任何值 都無法使纖維配向模型運算式符合所有配向模型元件。
經過檢查,Advani 與 Tucker 纖維配向模型形式有兩種方法可以控制纖維配向預測的準確度:
-
尋找更準確的閉合。
-
尋找能夠考慮閉合錯誤的新互動模型。
儘管第一種方法比較好用,但仍未發現任何閉合能夠令人滿意地將剪切與拉伸流的範圍包含在  的長時間範圍內 。
的長時間範圍內 。
閉合逼近所產生的影響是預測太多的平面外配向。此結果已由 Autodesk 所提出的纖維配向模型形式解決。