Moldflow 的纖維配向模型以 Folgar-Tucker 配向方程式為基礎。
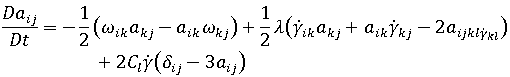
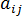 是纖維配向張量。
是纖維配向張量。 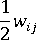 是旋度張量,而
是旋度張量,而 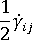 是變形率張量。
是變形率張量。  是纖維互動係數,即純量現象參數,其值透過調適到實驗結果來確定。此項已加入到原始 Jeffery 形式中來說明纖維之間的互動。
是纖維互動係數,即純量現象參數,其值透過調適到實驗結果來確定。此項已加入到原始 Jeffery 形式中來說明纖維之間的互動。
 ) 的另一項也已引入模型中:
) 的另一項也已引入模型中: 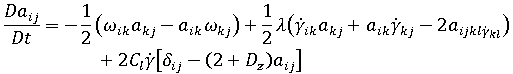
以下假設與考量因素適用於此修訂模型:
-
Folgar-Tucker 模型為濃縮懸浮液中的纖維配向預測提供了可接受的準確度。
-
會使用混合閉合,因為其形式簡單,且動態行為良好。
請注意以下幾點:
- 設定
 = 0.0 可將模型設定回 Jeffery 形式。
= 0.0 可將模型設定回 Jeffery 形式。 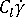 會影響配向張量。如果
會影響配向張量。如果 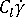 =0,纖維之間不會彼此互動;如果值 變得非常大,則纖維會變得比較不對齊。
=0,纖維之間不會彼此互動;如果值 變得非常大,則纖維會變得比較不對齊。 - 此
 項的大小可設定平面外方向中因纖維互動而產生的隨機影響重要性。
項的大小可設定平面外方向中因纖維互動而產生的隨機影響重要性。 - 設定
 = 1.0 可為 3D 問題提供 Folgar-Tucker 配向模型。設定
= 1.0 可為 3D 問題提供 Folgar-Tucker 配向模型。設定  = 0.0 可為 2D 問題提供 Folgar-Tucker 配向模型。
= 0.0 可為 2D 問題提供 Folgar-Tucker 配向模型。
但是,針對射出成型的情況,流的流體動力會導致纖維主要位於流平面中。它們在平面外旋轉的能力受到嚴格的限制。此機制會預測平面外方向纖維配向的隨機影響比平面內方向要小許多,因此會產生較小的  值。
值。
- 減小此
 參數:
參數: - 可減少平面外配向。
- 可增加公模仁層厚度。
- 模擬會將問題當成繞中間平面對稱來處理。
經驗  與比例 - 體積分率表示式
與比例 - 體積分率表示式
Bay 的實驗建議,Folgar 與 Tucker 的互動模型的確適用於射出成型問題。但是,使用者如何知道哪個  值可套用到纖維配向成型中?
值可套用到纖維配向成型中?
Folgar 與 Tucker 的實驗指出  取決於纖維體積分率及縱橫比,但相依性的形式不太清楚。
取決於纖維體積分率及縱橫比,但相依性的形式不太清楚。
膜狀澆口條中的流主要是簡單的剪切。薄殼層 (覆蓋從中間平面到壁的 40-90%) 應負責簡單剪切的穩定狀態值。此情況可為此相依性的檢查提供準備就緒的方法。
Bay 的薄殼層配向結果顯示,配向 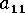 對纖維濃度非常敏感,指出可發展互動係數的經驗關係。此外,Bay 的測量也支持使纖維以與應變率成比例的比率散佈的提議。
對纖維濃度非常敏感,指出可發展互動係數的經驗關係。此外,Bay 的測量也支持使纖維以與應變率成比例的比率散佈的提議。
Bay 的論文中提供了一個運算式,為某些纖維詳細資料相關  互動係數的相依性提供了經驗關係。此運算式是一個簡單的指數
互動係數的相依性提供了經驗關係。此運算式是一個簡單的指數 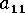 項。資料來自於不同材料 (PC、PBT、PA66) 的射出成型條之薄殼層,每種材料的等級為 6-7 玻璃等級。這些情況全都會被視為濃縮懸浮液。
項。資料來自於不同材料 (PC、PBT、PA66) 的射出成型條之薄殼層,每種材料的等級為 6-7 玻璃等級。這些情況全都會被視為濃縮懸浮液。
修正的經驗  表示式
表示式
根據薄殼層配向結果,對 Bay 表示式的預設 值對於各種玻璃含量的適用性進行了檢閱。
在  = 1.0 的條件下 (Folgar-Tucker 模型形式),
= 1.0 的條件下 (Folgar-Tucker 模型形式), 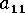 配向會過度預測針對兩種材料的所有玻璃含量。過度預測的等級會隨著玻璃含量的增加而減少。請見下圖。
配向會過度預測針對兩種材料的所有玻璃含量。過度預測的等級會隨著玻璃含量的增加而減少。請見下圖。
已使用末端澆口條及中心澆口圓盤執行了一系列的「纖維充填與保壓」分析驗證程序。針對兩種材料 (PA66 與 PBT) 的條紋薄殼層 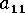 配向以及不同的玻璃等級進行了更詳細的考慮,並將結果與 Bay 的實驗配向資料進行了比較。配向等級一般為 0.8。
配向以及不同的玻璃等級進行了更詳細的考慮,並將結果與 Bay 的實驗配向資料進行了比較。配向等級一般為 0.8。
我們使用保壓階段結果對  的與已調整體積分率 cL / d (在
的與已調整體積分率 cL / d (在  = 0.01 與 1.0 時) 的經驗表示式進行了修訂。
= 0.01 與 1.0 時) 的經驗表示式進行了修訂。
對中間  值套用了更複雜的程序。
值套用了更複雜的程序。
下圖針對兩種材料在以下情況中的不同玻璃等級展示了薄殼圖層 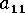 配向預測中的錯誤:
配向預測中的錯誤:
-
 = 0 (Jeffery 模型)。
= 0 (Jeffery 模型)。 - Bay 經驗表示式
 其中
其中  = 1.0 (Folgar-Tucker 模型)。
= 1.0 (Folgar-Tucker 模型)。 - 針對典型射出成型零件 (零件厚度 <; 2.5 mm),下面的圖表展示了修訂過的
 模型具有較低的
模型具有較低的  值,例如
值,例如  = 0.01 做為預設 (過去所提出)。
= 0.01 做為預設 (過去所提出)。 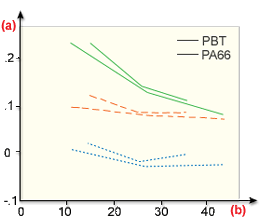
修訂
. 模型具有較低的
模型具有較低的  值
值(a) 錯誤;(b) % 玻璃 (重量);
 = 0.0 (Jeffery 模型);
= 0.0 (Jeffery 模型); Bay
Bay  (
(  =1.0);
=1.0); Moldflow 模型 (
Moldflow 模型 ( = 0.01)
= 0.01) - 針對較厚零件 (厚度 > 2.5 mm),會對修訂
 模型使用
模型使用  = 1.0。結果展示,
= 1.0。結果展示,  的值會隨零件厚度單調遞增。此一增加趨勢與平面外纖維配向隨著零件厚度增加而增加的預期一致。
的值會隨零件厚度單調遞增。此一增加趨勢與平面外纖維配向隨著零件厚度增加而增加的預期一致。
可進行以下觀察:
- Jeffery 與 Folgar-Tucker 模型傾向於導致在配向評估中發生過度預測。
- 低
 模型的情況對於薄零件 (厚度 < 2.5 mm) 會明顯降低錯誤等級。
模型的情況對於薄零件 (厚度 < 2.5 mm) 會明顯降低錯誤等級。 - 具有低
 值的預設 Bay 模型可針對高玻璃等級以外的等級提供 Bay 實驗資料可信帶之內的配向評估。
值的預設 Bay 模型可針對高玻璃等級以外的等級提供 Bay 實驗資料可信帶之內的配向評估。 - 修訂的模型針對考慮的材料與所有玻璃等級,比其他模型提供更為改善的配向預測。
針對  -
-  組合的摘要
組合的摘要
互動係數  的有效資料範圍為 0-1.0;但是,我們發現,相較於實驗結果,使用大於 0.1 的值並不會改善預測。
的有效資料範圍為 0-1.0;但是,我們發現,相較於實驗結果,使用大於 0.1 的值並不會改善預測。
互動係數  的厚度力矩的有效資料範圍為 0.0001-1.0。
的厚度力矩的有效資料範圍為 0.0001-1.0。
下表總結了本軟體版本所允許的互動係數與厚度力矩組合:
互動係數  |
互動係數的厚度力矩  |
備註 |
|---|---|---|
| 0 | 0.0001–1.0 |
|
0 <  <= 0.1 <= 0.1 |
1.0 | Folgar-Tucker 模型 |
| 預設 |  <= 1.0,(預設 = 1.0) <= 1.0,(預設 = 1.0) |
根據調整的體積分率 ( cL / d ) 從經驗式中衍生出  ,其中使用機械性質中的項與 ,其中使用機械性質中的項與 
 < 0.01 < 0.01 |
| 使用者設定 (0–0.1) |
 <= 1.0 <= 1.0 (預設 = 1.0) |
允許其他實作 |
纖維配向的分析方案概述
在成型製程中,某一點的纖維配向受到流體運動兩種不同方式的控制:流推論配向 (運動項) 及對流配向 (熱水平對流項)。
針對運動項,預測準確度取決於計算出來的速度梯度準確度。
針對熱水平對流項,其準確度取決於配向梯度的計算。與速度一樣,配向張量的表現法也視座標系而定。所有適用於計算速度梯度的數值方案也可以用來計算配向梯度。在纖維配向軟體中會使用相同的元素系統來表示速度與配向場,因此會使用相同的方案來計算速度與配向梯度。
現在介紹整體纖維配向方案的概要。纖維配向預測與模具充填模擬結合。
首先,演算法會開始充填與纖維配向計算。
然後會針對分析重複執行下列步驟,直到所有元素都凝固為止:
- 確定「充填與保壓」分析的時間步長
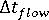 。
。 - 逐步推進流動波前。
- 計算壓力與速度場及應變張量。
- 計算平流項的穩定時間步長
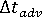 。
。 - 重複時間步長,直到
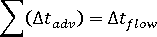 。
。 - 針對每一個元素中的每一個網格點:
- 計算平流纖維配向項,直到
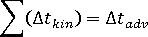 。
。 - 計算運動纖維配向項。
- 計算運動項的時間步長
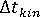 。
。 - 計算時間步長期間新的纖維配向
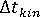 。
。
- 計算平流纖維配向項,直到
- 回到開始的步驟。