Die folgenden Annahmen werden bei der Entwicklung des Kriteriums für das Matrixkonstituentenversagen für unidirektionale Verbundwerkstoffe angewendet.
- Es wird davon ausgegangen, dass das Matrixversagen durch alle sechs Matrixdurchschnittsspannungskomponenten (
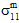 ,
, 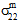 ,
, 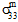 ,
, 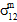 ,
, 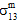 und
und 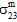 ) beeinflusst wird.
) beeinflusst wird. - Es wird weiter davon ausgegangen, dass das Matrixkonstituentenmaterial transversal isotrop ist. Daher lässt sich nicht unterscheiden, in welchem Maße
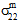 und
und 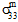 zum Matrixversagen beitragen, so wie auch nicht bestimmbar ist, wie unterschiedlich
zum Matrixversagen beitragen, so wie auch nicht bestimmbar ist, wie unterschiedlich 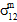 und
und 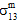 zum Matrixversagen beitragen.
zum Matrixversagen beitragen. - Inwieweit die Matrixdurchschnittsnormalspannungen (
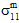 ,
, 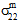 und
und 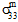 ) für das Matrixversagen verantwortlich sind, ist davon abhängig, ob es sich bei den Normalspannungen um Zug - oder Druckspannungen handelt.
) für das Matrixversagen verantwortlich sind, ist davon abhängig, ob es sich bei den Normalspannungen um Zug - oder Druckspannungen handelt. - Obwohl die Matrixkonstituenten als transversal isotrop bezeichnet werden, wird das Matrixversagen als ein isotropes Ereignis angenommen. Mit anderen Worten: Unabhängig von der jeweiligen Mischung von Spannungskomponenten, die für das Matrixversagen verantwortlich sind, bleibt die Auswirkung des Matrixversagens auf die Steifheit der Matrixkonstituenten unverändert. Genauer gesagt, wenn Matrixversagen auftritt, werden alle Matrixdurchschnittsmodule (
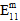 ,
, 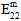 ,
, 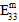 ,
, 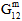 ,
, 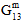 ,
, 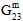 ) auf einen benutzerdefinierten Prozentsatz (Vorgabewert = 10 %) des ursprünglichen Werts reduziert, während die durchschnittlichen Poissonzahlen der Matrix (
) auf einen benutzerdefinierten Prozentsatz (Vorgabewert = 10 %) des ursprünglichen Werts reduziert, während die durchschnittlichen Poissonzahlen der Matrix (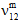 ,
, 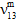 ,
, 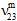 ) unverändert bleiben sollen.
Anmerkung: Dieses Steifheitsreduktionsschema bedeutet, dass unabhängig von der Kombination von Spannungskomponenten, die für das Auftreten von Matrixversagen verantwortlich sind, es nur einen Matrixausfallmodus gibt und eine einheitliche Degradation der Matrixsteifheit erfolgt.
) unverändert bleiben sollen.
Anmerkung: Dieses Steifheitsreduktionsschema bedeutet, dass unabhängig von der Kombination von Spannungskomponenten, die für das Auftreten von Matrixversagen verantwortlich sind, es nur einen Matrixausfallmodus gibt und eine einheitliche Degradation der Matrixsteifheit erfolgt.
Mit diesen vier grundlegenden Annahmen haben Forscher der University of Wyoming und von Firehole Composites (jetzt Autodesk) das folgende Matrixausfallkriterium entwickelt, das als quadratische Funktion der Matrixdurchschnittsspannungskomponenten ausgedrückt wird.
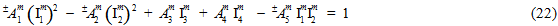
In Gleichung 22 sind die Größen 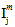 (j = 1,2,3,4) transversale isotrope Invarianten des Matrixdurchschnittsspannungszustands.
(j = 1,2,3,4) transversale isotrope Invarianten des Matrixdurchschnittsspannungszustands.
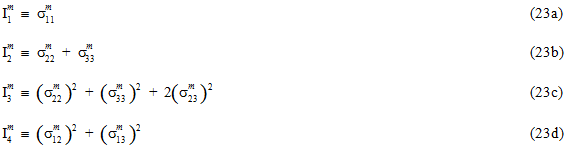
Die Größen 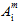 (i = 1,2,3,4,5) sind die anpassbaren Koeffizienten der Matrixausfallkriterien. In Gleichung 22 ein hochgestelltes Symbol '±' vor einem anpassbaren Koeffizienten
(i = 1,2,3,4,5) sind die anpassbaren Koeffizienten der Matrixausfallkriterien. In Gleichung 22 ein hochgestelltes Symbol '±' vor einem anpassbaren Koeffizienten 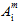 steht, bedeutet dies, dass der numerische Wert
steht, bedeutet dies, dass der numerische Wert 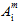 davon abhängt, ob die zugehörigen Matrixdurchschnittsspannungen Zug- oder Druckspannungen sind. Daher stellt
davon abhängt, ob die zugehörigen Matrixdurchschnittsspannungen Zug- oder Druckspannungen sind. Daher stellt 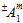 zwei mögliche Werte dar. Für den Koeffizienten
zwei mögliche Werte dar. Für den Koeffizienten 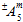 gibt es tatsächlich vier mögliche Werte, je nachdem, ob
gibt es tatsächlich vier mögliche Werte, je nachdem, ob 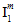 positiv oder negativ ist und auch, ob
positiv oder negativ ist und auch, ob 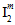 positiv oder negativ ist. Daher enthält das Matrixausfallkriterium (Gleichung 22) eine Gesamtanzahl von 10 anpassbaren Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials festgelegt werden.
positiv oder negativ ist. Daher enthält das Matrixausfallkriterium (Gleichung 22) eine Gesamtanzahl von 10 anpassbaren Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials festgelegt werden.