Auswirkung des Elementtyps auf die progressive Ausfallreaktion

Prognostizieren Sie die fortschreitende Ausfallreaktion der Verbundstruktur mit drei Finite-Element-Modellen.

Die Modelle unterscheiden sich lediglich hinsichtlich des Elementtyps, d. h., die Materialien, Netzdichte und Begrenzungsbedingungen sind in jedem Modell genau gleich. Drei Abaqus-Elementtypen werden getestet: C3D8R, C3D8 und SC8R. Jedes der drei Modelle verwendet die gleiche Gesamtdicken-Netzdichte. Für den Schaumkern wurden vier Elemente verwendet und jede Verbunddeckschicht ist in zwei Elemente unterteilt. Dies ergibt insgesamt 8 Elemente über die Gesamtdicke der Sandwichlage.

Modelle

ASCA_EP1_C3D8.inp

ASCA_EP1_SC8R.inp

Ergebnisse

Die folgende Tabelle gibt das Lastniveau an, für das die einzelnen Ausfallereignisse von den drei Modellen prognostiziert werden. Die folgende Abbildung zeigt alle Last-Vertikalverschiebungs-Kurven für die Verbundstruktur, die von den drei Modellen prognostiziert werden.

Anmerkung:
  1. Der Lastprozentsatz ist auf einer Skala von 0-100 % dargestellt.
  2. Globales Versagen wird als große Unterbrechung der Last-zu-Vertikalverschiebungs-Kurve für den 0°-Anwendungspunkt der vorher gezeigten Maximallast definiert.

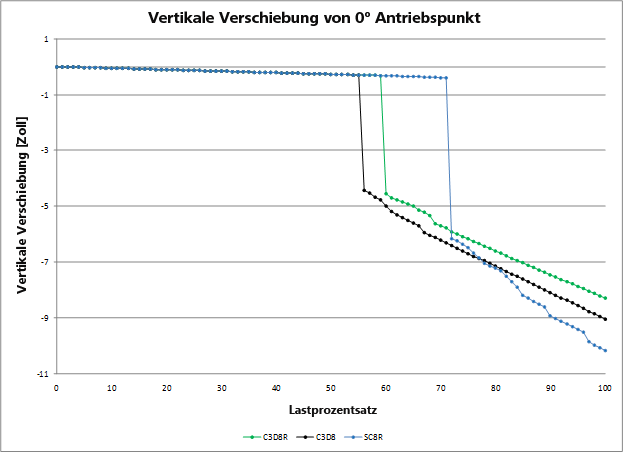
Beim Vergleichen von reduzierten Integrationskontinuumselementen mit vollständig integrierten Kontinuumselementen (C3D8R und C3D8) können die folgenden Beobachtungen und Erklärungen angegeben werden:

  1. Ein vollständig integrierter Elementtyp führt zu lokalen Ausfallereignissen (Matrix- und Faserausfall) bei niedrigen Lastniveaus.

    Das vollständig integrierte Element verwendet mehr Gaußsche Integrationspunkte als das reduzierte Integrationselement. Auch wenn beide Elemente dieselben durchschnittlichen Elementspannungen prognostizieren, prognostiziert das vollständig integrierte Element eine höhere lokale Spannungsspitze als das reduzierte Integrationselement, da es einfach mehr Gaußsche Integrationspunkte besitzt, die sich näher an den Begrenzungen befinden (an denen die lineare Spannungsverteilung den Höchstwert erreicht). Aus diesem Grund prognostiziert das vollständig integrierte Element den Beginn eines lokalisierten Ausfalls bei einem niedrigeren Niveau als das reduzierte Integrationselement.

  2. Der globale Ausfall tritt beim vollständig integrierten Kontinuumselement bei einem niedrigeren Lastniveau auf.

    Der Unterschied bei der Last des globalen Ausfalls, die von den beiden Elementen prognostiziert wird, beruht in erster Linie auf Unterschieden bei der Anfangslast des lokalen Ausfalls. Das reduzierte Integrationselement mit einem einzigen Gaußschen Punkt pro Materiallage bietet eine diskretisiertere Darstellung der Fehlerkaskade. Mit anderen Worten: Wenn in einer Materiallage eines reduzierten Integrationselements ein Materialausfall auftritt, reduziert sich die Steifheit der gesamten Lage und es tritt eine relativ große Lastneuverteilung auf. Wenn im Gegensatz dazu ein Ausfall an einem der Gaußschen Punkte in einer Materiallage eines vollständig integrierten Elements auftritt, verringert sich die Steifheit nur in einem Teil der Materiallage und es tritt eine relativ geringe Lastneuverteilung auf.

    Sie denken vermutlich, dass ein vollständig integriertes Element grundsätzlich eine realistischere fortschreitende Ausfallreaktion bietet, da es zahlreiche Integrationspunkte enthält, bei denen die Ausfallkriterien getestet werden und die Verringerung der Steifheit erzwungen wird. Dies ist nicht wahr, da die Integrationspunkte eines vollständig integrierten Elements nicht die genauesten Positionen für die Berechnung der Spannung darstellen. Tatsächlich stellen die reduzierten Integrationspunkte [1] die genauesten Positionen für die Berechnung der Spannung dar. Aus diesem Grund werten die reduzierten Integrationselemente den Ausfall und die Verringerung der Steifheit an weniger Punkten aus, aber die Auswertung selbst ist genauer, da der Spannungszustand an den reduzierten Integrationspunkten genauer ist. Daher führt die Verwendung von mehr Integrationspunkten pro Element nicht unbedingt zu einer genaueren Analyse.

Beim Vergleichen der Ausfallreaktion von reduzierten Integrationskontinuumselementen (C3D8R) mit reduzierten Integrationskontinuumsschalenelementen (SC8R) können die folgenden Beobachtungen und Erklärungen angegeben werden:

  1. Die Kontinuumsschalenelemente prognostizieren den Beginn eines lokalen Ausfalls bei geringeren Niveaus (42 %) als die reduzierten Integrationskontinuumselemente (52 %).

    Obwohl beide Elemente genau dieselben Gaußschen Integrationspunkte verwenden, prognostizieren die SC8R-Elemente höhere Spannungskomponenten in der Ebene als die C3D8R-Elemente. Diese Diskrepanz beruht auf Unterschieden bei der Querschersteifheit und der Quernormalensteifheit der beiden Elemente. Das C3D8R-Element erhält seine Quersteifheiten durch einfaches Integrieren der Steifheit der einzelnen Materiallagen in das Volumen des Elements. Das SC8R-Element erhält seine Quersteifheiten jedoch als direkte Benutzereingabe für das Element als Ganzes. Dieses Szenario schließt jedoch die Möglichkeit aus, dass beide Elemente dieselbe Quersteifheit aufweisen. Jede Änderung in der Quersteifheit eines Elements führt daher zwangsläufig zu einer anderen Aufteilung der Gesamtdehnungsenergie des Elements in Komponenten in der Ebene und außerhalb der Ebene. Wenn die beiden Elemente unterschiedliche Quersteifheiten aufweisen, haben sie daher wahrscheinlich unterschiedliche Spannungskomponenten in der Ebene. Bei diesem speziellen Problem wird der anfängliche Matrixausfall durch die Scherspannung in der Ebene gesteuert, die im SC8R-Element höher ist als im C3D8R-Element. Deshalb prognostiziert das SC8R-Element einen früheren lokalisierten Matrixausfall.

  2. Der globale Ausfall tritt beim Kontinuumsschalenelement bei einem höheren Lastniveau auf, obwohl lokale Ausfälle bei wesentlich niedrigeren Lastniveaus auftreten.

    Obwohl das SC8R-Element den Beginn eines lokalisierten Konstituentenausfalls bei einem niedrigeren Niveau als das C3D8R-Element prognostiziert, prognostiziert das SC8R-Element den globalen Strukturausfall bei einem höheren Lastniveau (72 %) als das C3D8R-Element (60 %). Die Tatsache, dass das SC8R-Element einen allmählicheren Fehlerkaskadenvorgang prognostiziert, beruht hauptsächlich darauf, dass sich lokalisierter Materialausfall nicht auf die Quersteifheiten (E33, G13, G23) im SC8R-Element auswirkt (Abaqus erfordert, dass diese Steifheiten im SC8R-Element konstant sind). Da für Quersteifheiten keine Degradation gilt, können sich die SC8R-Elemente einfacher an die Lastneuverteilung anpassen, ohne weitere lokalisierte Ausfälle zu verursachen. Zusammenfassend lässt sich sagen, dass die C3D8R- und SC8R-Elemente ein völlig unterschiedliches Fehlerkaskadenverhalten aufweisen.

Übergeordnetes Thema: Vergleichen von Modellen