Untersuchen Sie, wie schwankende Spannungen für die progressive Ermüdung verarbeitet werden.
Die Informationen auf den vorhergehenden Seiten stellen eine Methode zur Reduzierung des Spannungstensors auf einen einzelnen Skalarwert vor. Hier geht es jetzt darum, wie schwankende Spannungen zu berücksichtigen sind. Die Nomenklatur von Spannungsverhältnis R und der mittleren Spannung σm wird in der Regel hinzugefügt, um einfache sinusförmige Lasten zu beschreiben, die von der minimalen Spannung σ min bis zur maximalen Spannung σ max variieren können, wobei
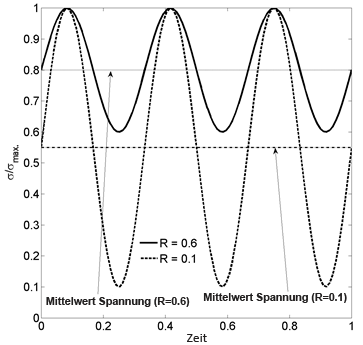
Beachten Sie die oben gezeigten Lastprotokolle für R = 0.1 und R = 0.6. Wenn Spannung die einzige, je nach Zeit variable Menge ist, kann die bindungsbrechende Rate als Funktion der Zeit geschrieben werden als
und die bindungsreparierende Rate kann wie folgt geschrieben werden:
Durch die Integration der Gleichungen 52 und 53 wird gezeigt, dass kinetische Theorie prognostiziert, dass die Erhöhung der mittleren Spannung σ min zu einer Verkürzung der Lebensdauer durch eine Erhöhung des Werts R führt. Von einem alternativen Standpunkt aus gesehen ist allerdings auch eine konstante Belastung R = 1 beachtenswert. Zwar ist offensichtlich, dass durch das Erhöhen der mittleren Spannung die Zeit bis zum Ausfall verkürzt wird. Aber Experimente mit unidirektionalen und gewebten Verbundwerkstoffen haben gezeigt, dass eine Erhöhung um σ min zu einer höheren Lebensdauer führt [47, 25-26]. Die Schwankungen der Spannung scheinen also ein zusätzliches physikalisches Element zu sein, dass bei konstanter Belastung nicht vorhanden ist.
Ein zusätzliches physikalisches Element ist die Temperaturänderung im Polymer während des Zyklus. Experimente mit reinen Polymeren haben gezeigt, dass eine deutliche Erwärmung des Polymers zusammen mit einem Anstieg der schwankenden Spannungsamplitude [28, 35] oder einer höheren Frequenz [48] erfolgt. Nach der kinetischen Theorie ist eine korrekte Prognose der Lebensdauer für jedes Lastprotokoll nur möglich, wenn diese Temperaturerhöhung berücksichtigt wird. Für einen Sinuszyklus wir die pro Sekunde verbrauchte Energie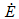 
festgelegt durch [28]:
wobei f die Oszillationsfrequenz ist, J" die Verlustkapazitanz und σa die Spannungsamplitude. Wir gehen davon aus, dass die Erhöhung der Temperatur proportional zur verbrauchten Energie ist. Die Temperatur T in Gleichung 40 wird berechnet aus der Nenntemperatur T* wobei
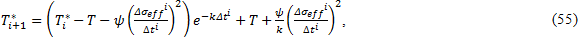
wobei ψ eine Proportionalitätskonstante ist, k die Konstante des Newtonschen Abkühlungsgesetzes, Δσeff die Größe der effektiven Spannungsänderung über einen Zeitraum Δt und n die Anzahl der unterschiedlichen Spannungsbereiche pro Zyklus [26]. Die Abbildung unten zeigt, wie die Werte Δσeff und Δt während eines einzelnen Lastzyklus festgelegt werden.
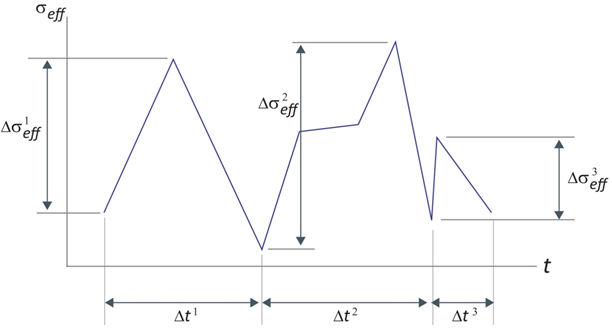
Mithilfe des Newtonschen Abkühlungsgesetzes in Gleichung 55 kann sich die Temperatur des Materials während eines langen Zeitraums an die Umgebungstemperatur angleichen, anstatt unbegrenzt anzusteigen.