Ermitteln der anfänglichen Bruchenergiewerte

Bestimmen Sie die verbrauchte Energie beim Verbundmaterial.

Wenn Sie die Funktion der energiebasierten Degradation (EBD) Simulation Composite Analysis verwenden möchten, sind zwei Werte erforderlich:

1. G^m: Die gesamte vor und nach einem Matrixausfall im Verbundwerkstoff verbrauchte Energie (Benutzermaterialkonstante 12).
2. G^f: Die gesamte in einem Verbundwerkstoff nach einem Faserausfall verbrauchte Energie (Benutzermaterialkonstante 14).

Die EBD-Funktion in Simulation Composite Analysis verwendet ein lineares Degradationsmodell, wie unten dargestellt.

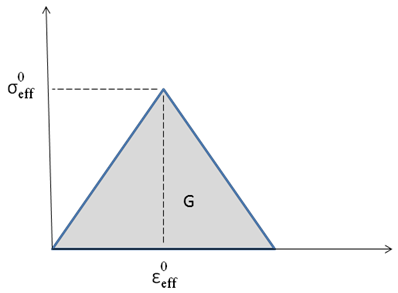
Gemäß der Abbildung oben kann die Gesamtenergie eines Elements ausgedrückt werden als

wobei 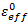der Wert für das effektive Dehnungsmaß von Verbundwerkstoffen bei Matrix- bzw. Faserausfall ist, 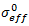das effektive Spannungsmaß von Verbundwerkstoffen bei Matrix- bzw. Faserausfall und V_e das Volumen des Elements.

Für die Matrixkonstituente wird 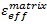ausgedrückt als

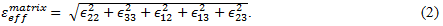
Für die Faserkonstituente wird 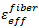ausgedrückt als

Die effektive Spannung der Matrixkonstituente, 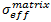, wird vergleichbar ausgedrückt als

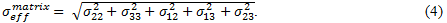
Die effektive Spannung der Faserkonstituente, 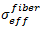, wird vergleichbar ausgedrückt als

In den Gleichungen 2 bis 5 stehen die Werte 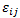und 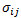für alle Verbundlagendehnungen und -spannungen. Um die bei Ausfall verbrauchte Energie zu schätzen, können die Werte für die Verbundlagendehnungen und -spannungen durch die Werte für die Ausfalldehnungen und -spannungen ersetzt werden. Die folgenden Festigkeitswerte (Ausfallspannung) sind verfügbar für IM7/8552:

1. ⁺S₁₁ = 362 ksi
2. ⁺S₂₂ = ⁺S₃₃ = 9.29 ksi
3. S₁₂ = S₁₃ = 13.2 ksi
4. S₂₃ = 13.8 ksi

Wenn keine Ausfalldehnungswerte verfügbar sind, kann das vereinfachte Hooke’sche Gesetz angewendet werden, um die Ausfalldehnung zu ermitteln. Dabei wird angenommen, dass die Materialreaktion vor dem Ausfall ungefähr linear ist,

Die folgenden E-Module (E) sind verfügbar für IM7/8552:

1. E₁₁ = 20 Msi
2. E₂₂ = E₃₃ = 1.42 Msi
3. G₁₂ = G₁₃ = 0.669 Msi
4. G₂₃ = 0.0475 Msi

Anhand der Materialeigenschaften für IM7/8552 und bei Ersetzung der Gleichung 6 durch die Gleichungen 2 und 3 können die folgenden effektiven Dehnungs- und Spannungswerte bei Ausfall für IM7/8552 berechnet werden:

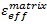1. = 0.0413
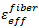2. = 0.0181
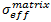3. = 26.7 ksi
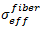4. = 362 ksi

In diesem Beispiel wurde ein Problem mit 2D-Schalenelementen erdacht, die nicht über ein Elementvolumen verfügen. Dieser Wert kann geschätzt werden, indem man die Elementfläche mit der Lagendicke multipliziert. Die Elementfläche lässt sich schnell bestimmen, indem man die globale Ausgangszahlgröße des Netzes, das dem Finite-Element-Modell zugeordnet ist, zum Quadrat nimmt. In diesem Beispiel wurde dem OHT-Modell eine globale Ausgangszahlgröße von 0.05 Zoll zugeordnet. Die für OHT verwendete Lage enthält 16 Schichten mit einer Schichtdicke von jeweils 0.0072 Zoll. Bei Verwendung dieser Werte wird ein Elementvolumen von 0.0115 Zoll³ berechnet.

Bei Eingabe des Elementvolumens, der effektiven Dehnung/Spannung für die Matrix und der effektiven Dehnung/Spannung für die Faser in Gleichung 1 ergeben sich die folgenden Energiewerte:

• G^m = 12.7 Zoll-lb.
• G^f = 75.5 Zoll-lb.

Diese beiden Werte werden für die Benutzermaterialkonstanten 12 und 14 bei Verwendung der energiebasierten Degradation eingegeben.