Die hier beschriebenen Annahmen werden zur Entwicklung des Ausfallkriteriums für Faserkonstituenten verwendet.
- Es wird angenommen, dass Faserausfälle von den gemittelten Spannungskomponenten für die Faserkonstituente
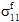 ,
, 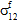 und
und 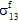 beeinflusst werden.
beeinflusst werden. - Es wird angenommen, dass Faserausfälle von den gemittelten Spannungskomponenten für die Faserkonstituente
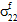 ,
, 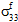 und
und 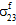 unabhängig sind.
unabhängig sind. - Der Beitrag von
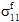 zur Produktion von Faserausfällen ist davon abhängig, ob
zur Produktion von Faserausfällen ist davon abhängig, ob 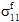 eine Zug - oder Druckspannung darstellt.
eine Zug - oder Druckspannung darstellt. - Für die Faserkonstituente wird ein transversal isotropes Verhalten angenommen. Folglich kann zwischen den Beiträgen von
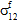 und
und 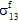 zum Faserausfall nicht unterschieden werden.
zum Faserausfall nicht unterschieden werden. - Bei unidirektionalen Verbundmaterialien wird für die Faserkonstituente ein transversal isotropes Material angenommen. Der Faserausfall hingegen wird als isotropes Ereignis betrachtet. Anders ausgedrückt: Unabhängig von der jeweiligen Kombination von Spannungskomponenten, die für den Faserausfall verantwortlich sind, bleibt die Auswirkung des Faserausfalls auf die Steifheit der Faserkonstituente dieselbe. Das heißt insbesondere, dass bei Faserausfall die faserbezogenen Durchschnitts-Module (
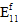 ,
, 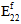 ,
,  ,
, 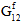 ,
,  und
und 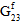 ) auf einen benutzerdefinierten Prozentsatz ihrer ursprünglichen Werte (die Vorgabe ist 1 %) reduziert werden, während für die faserbezogenen durchschnittlichen Poissonzahlen (
) auf einen benutzerdefinierten Prozentsatz ihrer ursprünglichen Werte (die Vorgabe ist 1 %) reduziert werden, während für die faserbezogenen durchschnittlichen Poissonzahlen (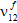 ,
, 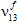 und
und 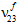 ) angenommen wird, dass sie unverändert bleiben.
Anmerkung: Dieses Steifheitsreduktionsschema bedeutet, dass es unabhängig von der Kombination von Spannungskomponenten, die Faserausfälle verursachen, nur einen Faserausfall-Modus gibt und dieser zu einer einheitlichen Reduktion der Fasermodule führt.
) angenommen wird, dass sie unverändert bleiben.
Anmerkung: Dieses Steifheitsreduktionsschema bedeutet, dass es unabhängig von der Kombination von Spannungskomponenten, die Faserausfälle verursachen, nur einen Faserausfall-Modus gibt und dieser zu einer einheitlichen Reduktion der Fasermodule führt. - Bei gewebten Verbundmaterialien wird für den Faserausfall ein orthotropes Ereignis angenommen. Insbesondere werden
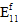 ,
, 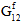 und
und  reduziert, während
reduziert, während 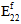 ,
,  und
und 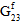 unverändert bleiben.
unverändert bleiben.
Auf der Basis dieser fünf grundlegenden Annahmen haben Forscher von der University of Wyoming und Firehole Composites (jetzt Autodesk) das folgende Faserausfallkriterium entwickelt, welches als quadratische Funktion der gemittelten Faserspannungskomponenten ausgedrückt wird.

Die Größen  (i = 1,4) sind zwei der transversal isotropen Invarianten des faserbezogenen durchschnittlichen Spannungszustands.
(i = 1,4) sind zwei der transversal isotropen Invarianten des faserbezogenen durchschnittlichen Spannungszustands.

Die Größen 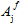 (j 1,4) sind die anpassbaren Koeffizienten des Faserausfallkriteriums. In Gleichung 26 weist ein hochgestelltes Symbol "±"' vor dem Koeffizienten
(j 1,4) sind die anpassbaren Koeffizienten des Faserausfallkriteriums. In Gleichung 26 weist ein hochgestelltes Symbol "±"' vor dem Koeffizienten 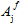 darauf hin, dass der Wert davon abhängt, ob sich die durchschnittlichen Faserspannungen auf Zug - oder Druckspannung beziehen.
darauf hin, dass der Wert davon abhängt, ob sich die durchschnittlichen Faserspannungen auf Zug - oder Druckspannung beziehen. 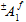 steht daher für zwei mögliche Werte. Folglich enthält das Faserausfallkriterium (Gleichung 26) insgesamt drei anpassbare Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials ermittelt werden müssen.
steht daher für zwei mögliche Werte. Folglich enthält das Faserausfallkriterium (Gleichung 26) insgesamt drei anpassbare Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials ermittelt werden müssen.
Zusammen genommen enthalten die Ausfallkriterien für die Matrix- und Faserkonstituenten insgesamt 13 anpassbare Koeffizienten für unidirektionale Verbundmaterialien und sechs anpassbare Koeffizienten für gewebte Verbundmaterialien. Das Verfahren zur Bestimmung der Werte für diese Koeffizienten wird später beschrieben (siehe Ausfallkriterien für unidirektionale Verbundmaterialien).