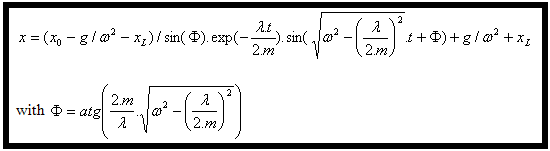Einer der wichtigsten Schritte bei der Konstruktion ist die Überprüfung. Bei der Überprüfung einer Konstruktion ist es häufig empfehlenswert, einfache, zuverlässige theoretische Beispiele als Maßstab zu verwenden. Nachfolgend finden Sie einige dieser Beispiele.
Diese Beispiele beschreiben die Gleichungen und Annahmen, die zur Überprüfung einer Simulationsausgabe verwendet werden.
Verschiebung, das Masse-Feder-Beispiel
Ein Beispiel mit einfacher Masse und Federüberprüfung.

Newton'sche Gesetz:
![]() (1)
(1)
Mit:
| Numerischer Wert: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
mit |
|
|
|
|
|
Eine Lösung für diese Differentialgleichung ist: |
|
|
|
|
|
Eine besondere Lösung, wenn das System stabilisiert ist, ist für |
|
|
Dann gilt: (2) |
|
|
|
|
|
|
|
|
Die Anfangsbedingungen bestimmen den Wert von A und |
|
|
für t = 0.0, (3) |
|
|
|
|
|
und |
|
|
|
|
|
(4) und (6), angegeben in (3), ergeben die Gleichung der Verschiebung : |
|
|
|
|
|
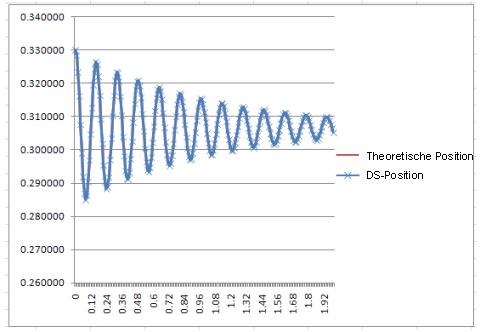
Diese Gleichung wurde dann in Excel programmiert und die Ergebnisse mit dem der dynamischen Simulation verglichen, die Ergebnisse sind identisch. |
|
 |
|
Position und Geschwindigkeit, das Kurbelwelle-Kolben-Beispiel
Der Zweck dieses Überprüfungsbeispiels besteht darin, die Position und Geschwindigkeit in einem Mechanismus bestehend aus Kurbelwelle und Kolben zu überprüfen, wenn die Ausgaben aus der dynamischen Simulation im Vergleich zu theoretischen Gleichungen das Gleiche beschreiben.
Bekannte Werte: Der Hub bzw. der Abstand des Kurbelwellenzapfens vom Drehmittelpunkt der Kurbelwelle und die Länge der Kurbelstange zwischen dem Hauptwellenlager und dem Kolbenbolzengelenk.
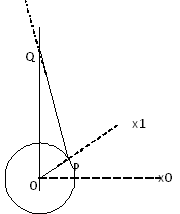
Diagramm
|
Definition |
R = Länge(OP) = Kurbelwellenhub L = Länge(PQ) = Länge der Kurbelstange |
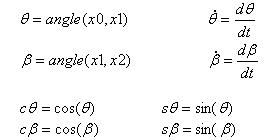 |
|
|
Geschwindigkeit von Punkt Q in Abhängigkeit zum absoluten Koordinatensystem R0 = (x0, y0) |
|
|
|
// Position von Q in R0 |
|
|
// Geschwindigkeit von Q in R0 |
| mit:
|
|
| und:
|
|
|
|
|
| mit: |
|
| und: |
|
| dann: |
|
|
Punkt Q verbleibt auf der y0-Achse und die x0-Komponente beträgt 0.0: |
|
|
|
|
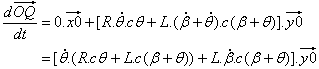 |
|
| Bei Verwendung von (1): | |
|
|
|
|
Gleichung (1) ergibt |
|
|
(1) |
|
und 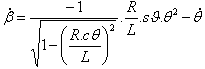 |
|
| Mit MS Excel und numerischen Werten (L=0.125m, R=0.06m und |
|
|
Position: |
|
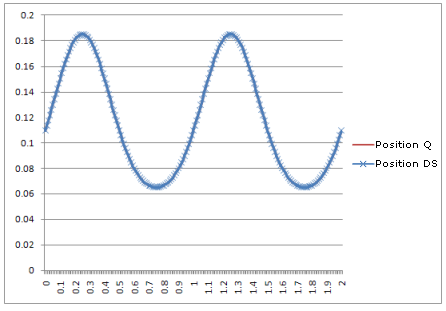 |
|
|
Geschwindigkeit: |
|
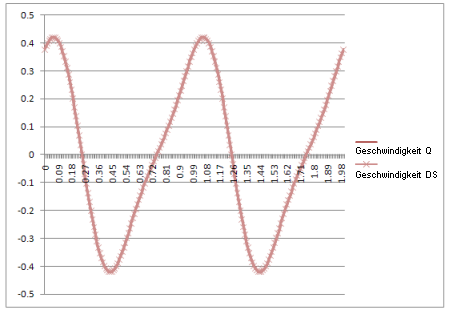 |
|
Das Ergebnis: Kurven in der dynamischen Simulation sind identisch mit den mit den theoretischen Gleichungen erstellten Kurven.
 (3)
(3)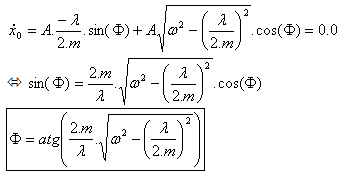 (5)
(5)