Für den Fall, bei dem ohmsche oder Joule-Erwärmung berücksichtigt werden soll, gilt die folgende Energiegleichung für inkompressible Strömung:
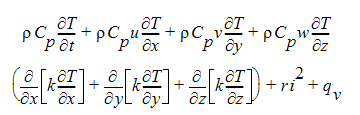
wobei i die Größe der aktuellen Dichte und r der elektrische Widerstand (eine Materialeigenschaft) ist. Mit dieser Gleichung muss auch eine Gleichung zur Bestimmung des elektrischen Stroms in dem ohmschen Term ri2 gelöst werden. Wir verwenden die elektrische Potenzialgleichung:
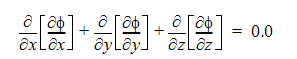
wobei das elektrische Potenzial ist und der Strom berechnet wird mit:
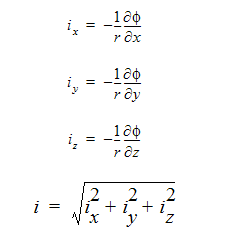
Die Variablen in diesen Gleichungen werden in der folgenden Tabelle definiert:
| Variable | Beschreibung (Beispieleinheiten, SI-System) |
| Cp | Konstanter Druck spezifische Wärme (J/kg-K) |
| i | Elektrische Stromdichte (A/m2) |
| k | Wärmeleitfähigkeit (W/m-K) |
| qv | Volumetrische Wärmequelle (W/m3) |
| r | Elektrischer Widerstand (Ohm-m) |
| T | Temperatur (K) |
| t | Zeit (s) |
| u | Geschwindigkeit in X-Richtung (m/s) |
| v | Geschwindigkeit in Y-Richtung (m/s) |
| w | Geschwindigkeit in Z-Richtung (m/s) |
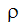
|
Dichte (kg/m3) |
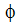
|
Elektrisches Potenzial (Spannung) |
Die Randbedingungen für die Energiegleichung umfassen die üblichen Angaben: Temperatur, Wärmeübergangskoeffizient, Wärmestrom oder Wärmestrahlung in einer externen Quelle. Die Randbedingungen für die elektrische Potenzialgleichung enthalten eine angegebene Spannung oder einen angegebenen elektrischen Strom.