Add constraints to create rules that control how a part can change in shape or size.
Depending on the geometry of the model, you may need to add one or more constraints to define the shape or size of the model. Constraints enforce rules that you want the model to obey. Constraining a model controls how a model can change in shape or size, called “degrees of freedom.” For example, a circle has two degrees of freedom: the location of its center and its diameter. If the center and diameter are defined, the circle is fully constrained and those values can be maintained. Constraints specify the relationships of geometric features; for example, whether two features are perpendicular, parallel, straight, concentric, or have the same midpoint or radius.
Constraints work in conjunction with dimensions to control the shape and size of the model. Any time you modify the model, the geometry retains the relationships among features in accordance with the applied constraints. You add constraints to indicate your design intent. For example, a parallel constraint could be defined between two lines based on the geometry of the model. You could also add a constraint to force both lines to have the same length.
As you apply geometric constraints, continue to analyze the model, reviewing and replacing constraints as necessary. As you gain experience, you will be able to determine which constraints control the model to meet your design requirements. Some constraints work only with lines, while others work only with arcs, circles, or points.
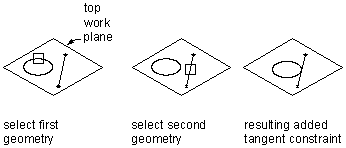
Applying a straight constraint
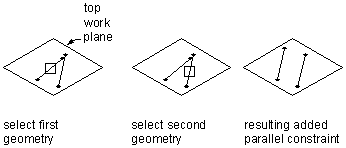
Applying a parallel constraint
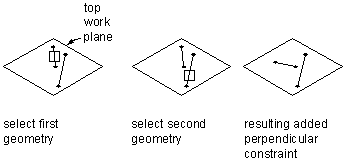
Applying a perpendicular constraint
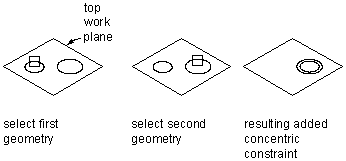
Applying a concentric constraint
Part Builder provides ten geometric constraints. The following list describes these constraints and the features with which they can be used.
- Straight
-
Can be defined between curved geometry (such as a circle or arc) and either another curved geometry or a line. Makes two curves tangential to one another, even if they do not physically share a point. Tangency is commonly used to constrain a line to an arc or circle.
- Parallel
-
Can be defined between pairs of geometry with a direction, such as lines. Causes two or more lines to be parallel to one another.
- Perpendicular
-
Can be defined between pairs of geometry with a direction, such as lines. Causes selected lines to lie at right angles to one another.
- Concentric
-
Can be defined for any combination of circles and points. Fixes the centers of the geometry to the same location. Common uses include circle to circle, where the center of both circles is the same; circle to point, where the point lies at the center of the circle; and point to point, where the points are the same.
- Coincident
-
Can be defined between a point and any geometry. Fixes two points (including center points) together; essentially, the point lies on the geometry.
- Equal Distance
-
Can be defined between two pairs of geometry. The distance between the first pair of geometries is fixed to the distance between the second pair. Equal distance constraints do not control the actual distance. Each pair of geometries must be one of the following: any combination of points and lines, two circles or arcs concentrically constrained, or a point and circle or arc concentrically constrained.
- Equal Radius
-
Can be defined between two circles or two arcs. Fixes the radius of both circles or arcs to be of the same value. Equal radius constraints do not control the value of the radii.
- Midpoint
-
Can be defined between a point and either two other points or two lines. The point is equal distance from the other two geometries. Midpoint constraints do not control the distance. A common use is constraining a point to the middle of a line.
- Symmetric
-
Can be defined between two geometries of the same type and a line. The two geometries are symmetrically arranged on opposite sides of the line. The symmetric constraint does not force constrained geometry to maintain an exact mirror image.
- Normal
-
Can be defined between a line or curve and a curve. (Two lines cannot be made normal; a perpendicular constraint must be used instead.) The curves intersect and the directions of curve straights are perpendicular at the intersection point. A common use is constraining a line to the normal of an ellipse.