Use Discretizator to make float or integer values more discrete, reducing a wide range of values to a more manageable subset at the cost of a certain amount of accuracy. This helps in potential optimization of the input data for the Shape Control suboperator but can be used for other purposes as well.
The discretization is based on two values: Base and Step. For each incoming value, the Step value is multiplied by an positive or negative integer and then added to the Base value in order to bring the result as close as possible to the input; the input is then rounded to this value. With Base "b" and Step "s," the possible output values from the suboperator are b, b+s, b–s, b+2s, b–2s, b+3s, b–3s, and so on.
The incoming values are rounded to the closest discrete value. If incoming value is exactly between the discrete values, it's rounded up to the next-highest value. For example, with Base 0 and Step 1, the input value 1.5 is output as 2, and input value –1.5 becomes –1.
Example of Discretizator Usage
You can find an example of Discretizator usage in the included file GridAndShapeControl.max. The flow contains more than 10,000 particles and incorporates two Data operators, both disabled at the beginning.
The first Data Operator does not use Discretizator; turn it on and note how long it takes to calculates the geometry shapes for all particles. It’s pretty slow, even on a fast PC.
Next, turn off the first Data operator and turn on the second one. It uses Discretizator in the data flow, and it works much faster when generating particle shapes. This is because the operator makes the incoming data stream discrete with the step of 1 degree. In the first case, the shape is calculated individually for each particle. In the second case the set of possible values is significantly reduced because values are snapped to whole degrees. Because Discrete Optimization is on in the Shape Control suboperator in the second Data Operator, the shapes are generated for 360 particles at most; this is the greatest possible number of different angle values with the step of 1 degree, and then these shapes are shared between particles. The eye cannot distinguish between these two cases, but the second one works much faster.
Thus, the Discretizator suboperator is a useful optimization tool for the Shape Control suboperator.
Interface
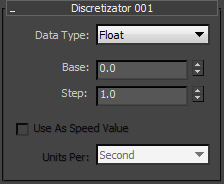
- Data Type
- The expected incoming data type. This setting determines the number system available for the Base and Step parameters.
- Base
- The “starting point” for the discretization process. For details, see the introduction to this topic.
- Step
- This value is added to or subtracted from the Base value repeatedly until the result is as close as possible to the input value. For details, see the introduction to this topic.
- Use As Speed Value
- Internally, the speed of particles in a Particle Flow system is presented in units per tick (4800 ticks = 1 sec). However, the speed parameters in Particle Flow operators are presented as units per second. To translate from the displayed values to internal values, to turn On Use As Speed Value and use the default setting Units Per Second. This way you can access, for example, the speed defined by the standard Speed operator in Particle Flow. Available only when the input parameter is of the Real type.