NURBS curves and surfaces did not exist in the traditional drafting world. They were created specifically for 3D modeling using computers. Curves and surfaces represent contours or shapes within a 3D modeling space. They are constructed mathematically.
NURBS mathematics is complex, and this section is simply an introduction to some NURBS concepts that might help you understand what you are creating, and why NURBS objects behave as they do. For a comprehensive description of the mathematics and algorithms involved in NURBS modeling, see The NURBS Book by Les Piegl and Wayne Tiller (New York: Springer, second edition 1997).
Definition and Parameter Space
The term NURBS stands for Non-Uniform Rational B-Splines. Specifically:
- Non-Uniform means that the extent of a control vertex's influence can vary. This is useful when modeling irregular surfaces.
- Rational means that the equation used to represent the curve or surface is expressed as a ratio of two polynomials, rather than a single summed polynomial. The rational equation provides a better model of some important curves and surfaces, especially conic sections, cones, spheres, and so on.
- A B-spline (for basis spline) is a way to construct a curve that is interpolated between three or more points.
Shape curves such as the Line tool and other Shape tools are Bezier curves, which are a special case of B-splines.
The non-uniform property of NURBS brings up an important point. Because they are generated mathematically, NURBS objects have a parameter space in addition to the 3D geometric space in which they are displayed. Specifically, an array of values called knots specifies the extent of influence of each control vertex (CV) on the curve or surface. Knots are invisible in 3D space and you can't manipulate them directly, but occasionally their behavior affects the visible appearance of the NURBS object. This topic mentions those situations. Parameter space is one-dimensional for curves, which have only a single U dimension topologically, even though they exist geometrically in 3D space. Surfaces have two dimensions in parameter space, called U and V.
NURBS curves and surfaces have the important properties of not changing under the standard geometric affine transformations (Transforms), or under perspective projections. The CVs have local control of the object: moving a CV or changing its weight does not affect any part of the object beyond the neighboring CVs. (You can override this property by using the Soft Selection controls.) Also, the control lattice that connects CVs surrounds the surface. This is known as the convex hull property.
Degree and Continuity
All curves have a degree. The degree of a curve is the highest exponent in the equation used to represent it. A linear equation is degree 1; a quadratic equation is degree 2. NURBS curves typically are represented by cubic equations and have a degree of 3. Higher degrees are possible, but usually unnecessary.
Curves also have continuity. A continuous curve is unbroken. There are different levels of continuity. A curve with an angle or cusp is C 0 continuous: that is, the curve is continuous but has no derivative at the cusp. A curve with no such cusp but whose curvature changes is C 1 continuous. Its derivative is also continuous, but its second derivative is not. A curve with uninterrupted, unchanging curvature is C 2 continuous. Both its first and second derivatives are also continuous.

Levels of curve continuity:
Left: C 0 , because of the angle at the top
Middle: C 1 , at the top a semicircle joins a semicircle of smaller radius
Right: C 2 , the difference is subtle but the right side is not semicircular and blends with the left
A curve can have still higher levels of continuity, but for computer modeling these three are adequate. Usually the eye can't distinguish between a C 2 continuous curve and one with higher continuity.
Continuity and degree are related. A degree 3 equation can generate a C 2 continuous curve. This is why higher-degree curves aren't generally needed in NURBS modeling. Higher-degree curves are also less stable numerically, so using them isn't recommended.
Different segments of a NURBS curve can have different levels of continuity. In particular, by placing CVs at the same location or very close together, you reduce the continuity level. Two coincident CVs sharpen the curvature. Three coincident CVs create an angular cusp in the curve. This property of NURBS curves is known as multiplicity. In effect, the additional one or two CVs combine their influence in that vicinity of the curve.
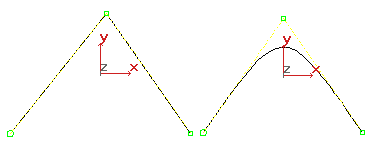
Effects of multiplicity: there are three CVs at the apex on the left, two CVs at the apex on the right.
By moving one CV away from the other, you increase the curve's continuity level again. Multiplicity also applies when you fuse CVs. Fused CVs create a sharper curvature or a cusp in the curve. Again, the effect goes away if you unfuse the CVs and move one away from the other.
Degree, continuity, and multiplicity apply to NURBS surfaces as well as to curves.
Refining Curves and Surfaces
Refining a NURBS curve means adding more CVs. Refining gives you finer control over the shape of the curve. When you refine a NURBS curve, 3ds Max preserves the original curvature. In other words, the shape of the curve doesn't change, but the neighboring CVs move away from the CV you add. This is because of multiplicity: if the neighboring CVs didn't move, the increased presence of CVs would sharpen the curve. To avoid this effect, first refine the curve, and then change it by transforming the newly added CVs, or adjusting their weights.
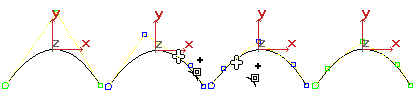
Refining a NURBS curve.
NURBS surfaces have essentially the same properties as NURBS curves, extended from a one-dimensional parameter space to two dimensions.
Reparameterizing CV Curves and Surfaces
When you refine a NURBS curve or surface, it is a good idea to reparameterize it. Reparameterizing adjusts the parameter space so the curve or surface will behave well when you edit it in viewports. There are two ways to reparameterize:
- Chord-length
Chord-length reparameterization spaces knots in parameter space based on the square root of the length of each curve segment.
- Uniform
Uniform reparameterization spaces knots uniformly. A uniform knot vector has the advantage that the curve or surface changes only locally when you edit it.
CV curve and surface sub-objects give you the option of reparameterizing automatically whenever you edit the curve or surface.
Point Curve and Surface Concepts
You can work with point curves and point surfaces as well as with CV curves and surfaces. The points that control these objects are constrained to lie on the curve or surface. There is no control lattice, and no weight control. This is a simpler interface that you might find easier to work with. Also, point-based objects give you the ability to construct curves based on dependent (constrained) points, and then use these to construct dependent surfaces.
You can think of point curves and surfaces as an interface to CV curves and surfaces, which are the fully defined NURBS objects. The underlying representation of the curve or surface is still constructed using CVs.
You can also think of a point curve or surface as dependent on its points. You can use the Convert Curve button to convert a point curve or surface to the CV form, or vice versa.