Matrix Constituent Failure Criterion (Unidirectional Composites)

The assumptions that follow are employed in the development of the matrix constituent failure criterion for unidirectional composites.

1. Matrix failure is assumed to be influenced by all six of the matrix average stress components , , 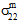, , 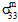, 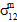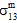and .
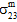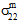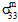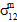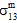2. The matrix constituent material is assumed to be transversely isotropic; consequently, you cannot distinguish between the contributions of and to matrix failure, nor can you distinguish between the contributions of and to matrix failure.
3. The influence of the matrix average normal stresses (, , 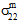and 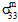) in producing matrix failure depends upon whether the normal stresses are tensile or compressive.
4. Although the matrix constituent is considered transversely isotropic, matrix failure is assumed to be an isotropic event. In other words, regardless of the particular mix of stress components responsible for producing matrix failure, the effect of matrix failure on the stiffness of the matrix constituent remains the same. Specifically, when matrix failure occurs, each of the matrix average moduli (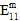, , 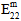, , 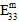, 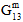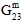) are reduced to a user-defined percentage (default value = 10%) of their original values, while the matrix average Poisson ratios (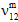, , 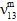) are assumed to remain unchanged.
   Note: This stiffness reduction scheme implies that, regardless of the combination of stress components causing matrix failure to occur, there is only one matrix failure mode and it results in a uniform degradation of matrix stiffness.

Using these four basic assumptions, researchers from the University of Wyoming and Firehole Composites (now Autodesk) have developed the following matrix failure criterion that is expressed as a quadratic function of the matrix average stress components.

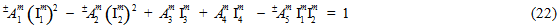
In Eq. 22, the quantities 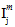(j = 1,2,3,4) are transversely isotropic invariants of the matrix average stress state.

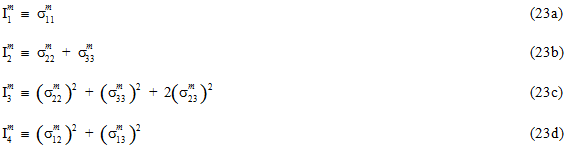
The quantities 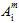(i = 1,2,3,4,5) are the adjustable coefficients of the matrix failure criteria. In Eq. 22, if a superscript symbol '±' precedes an adjustable coefficient 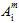, it indicates that the numerical value of 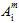depends on whether the associated matrix average stresses are tensile or compressive; hence 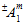represents two possible values. For the coefficient , there are actually four possible values depending on whether 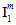is positive or negative and also on whether 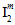is positive or negative. Therefore, the matrix failure criterion (Eq. 22) contains a total of 10 adjustable coefficients that must be determined using measured strengths of the composite material.