The plasticity response of the matrix constituent material is defined collectively by Eqs. 1-8. However, the model must also utilize a rupture criterion that identifies complete failure of the short fiber filled material. We assume the functional form of the effective stress expression (a weighted von Mises stress, see Eq. 6) is sufficient to define the directional dependency of the material for both the prediction of matrix plastic evolution and the prediction of matrix rupture. Therefore, the determination of the matrix rupture criterion requires that we simply establish an upper limit on the value of the weighted effective stress measure (denoted the effective strength Seff). In this case, the matrix rupture condition is expressed as
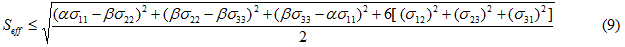
where it is understood that the stress components represent the average stress in the matrix constituent material.
- There is no longer any need to decompose the composite stress and strain into matrix stress and strain since we no longer have to compute plastic evolution for the matrix.
- The constitutive relations of the homogenized composite material are used directly instead of building the composite constitutive relations from the constituent constitutive relations and microstructure (as seen earlier).
- The stiffness of the composite material is instantaneously reduced to a fraction of the original elastic stiffness of the composite material. This stiffness reduction is performed by multiplying all six of the original composite moduli by a degradation constant. Note, that once the rupture condition is triggered, the stiffness of the composite material remains fixed at the reduced value for the duration of the simulation.
- The composite constitutive relations are switched from a tangent formulation (which was used during the plasticity phase of the material response) to a secant formulation. Since the stiffness of the failed composite material remains fixed, the integration point in question no longer makes any direct contribution to the nonlinearity of the solution.