In order to use the multiscale material model for short fiber filled materials described in the preceding pages, we must first determine the value of the model's coefficients by fitting the model to a collection of experimental data for the material in question. Ideally, to allow for a definitive fitting of the model's coefficients, the collection of experimental data should cover the full range of behavior that can be exhibited by the material. However, from a practical point of view, it is highly desirable to limit both the number and complexity of the tests that have to be conducted.
With the current model, good fits can be obtained by using three different tensile tests to failure. The image below shows such a collection of tensile tests and includes data from tensile loading at three different directions relative to the average fiber direction of a mostly-aligned material. The tensile tests include 0°, 45°, and 90° specimens. In each case, the specimen is loaded until final rupture occurs.
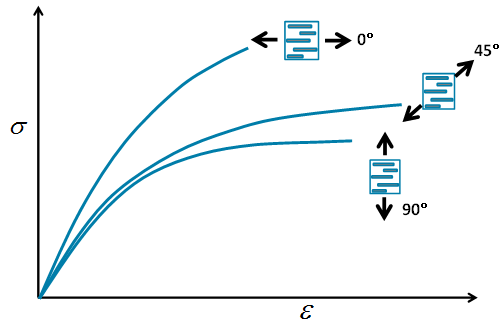
The model coefficients that must be determined include four elastic coefficients and four plastic coefficients. The elastic coefficients include the modulus and Poisson ratio of the matrix constituent and the modulus and Poisson ratio of the fiber constituent. The four plastic coefficients include σ0, n, α, and β.
- The four elastic coefficients are determined by requiring the model to accurately represent the initial elastic responses of the 0°, 90°, and 45° tensile test specimens (as provided by the first few data points from each of the three tensile tests).
- The four plastic coefficients are fit to allow the model to accurately represent the full response history of all three tensile tests.