The process of establishing the effective strength needed for the rupture criterion (Eq. 9) begins with an examination of the 0°, 90°, and 45° tensile test data sets to identify the load level at which each specimen ruptures. These load levels will be denoted L0, L90, and L45 for the 0°, 90°, and 45° tensile test specimens respectively. Next, the model is used (with optimized elasticity and plasticity coefficients) to simulate each of the three tensile tests.
For the 0° tensile test, when the model reaches the load level L0, the model is used to compute the effective stress in the matrix that corresponds to the rupture event (this effective stress is denoted the effective strength Seff_0). Similarly, the model is used to simulate the 45° and 90° tensile tests to establish Seff_45 and Seff_90 respectively.
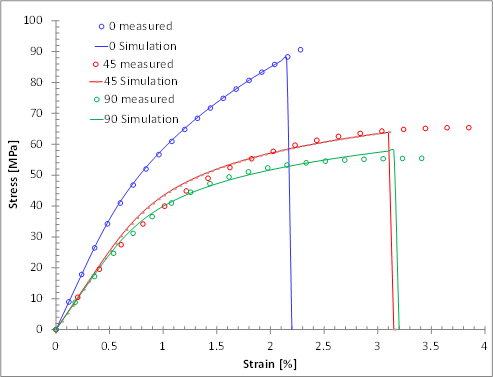
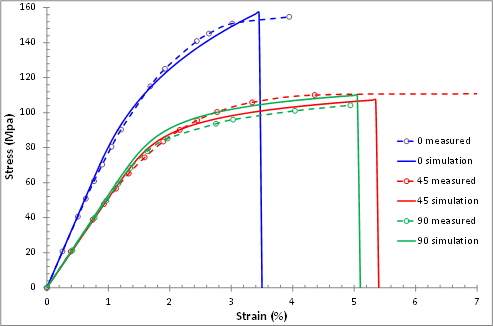
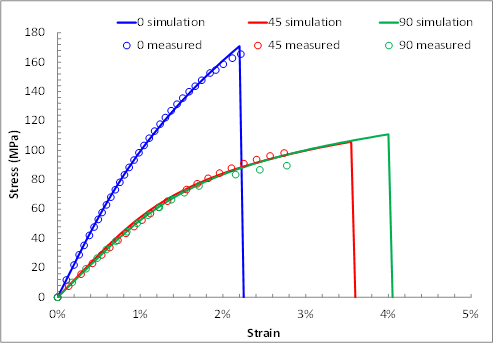
If the weighted effective matrix stress was strongly relevant to the prediction of matrix rupture, we would expect that the values of Seff_0, Seff_45, and Seff_90 would be similar. In fact, in all cased examined thus far, the range of the three values (Seff_0, Seff_45, Seff_90) has been less than 10% of the mean value. This indicates that the weighted effective matrix stress is indeed a good predictor of matrix rupture.
There are many ways the effective strength Seff (of Eq. 9) could be determined from the set of values Seff_0, Seff_45, and Seff_90. Here we simply use Seff ≡ Seff_0 because it is deemed important to ensure the rupture condition of the 0° tensile test is accurately captured. We anticipate that the injection molding process is designed to ensure the primary tension/compression load paths have fibers that are mostly aligned with the load path. Therefore, the rupture of an injection molded part will be most accurately predicted if the 0° tensile test rupture condition can be accurately simulated.
Note, the rupture strength (Eq. 9) is formulated for a mostly-aligned material. In fact, a Moldflow simulation of the injection molded plaques that the tensile test specimens are cut from typically reveals that the fiber filled material exhibits a degree of alignedness of approximately λI = 0.85. However, the rupture criterion (Eq. 9) must account for the strength of the material regardless of the degree of fiber alignedness. Note that the rupture criterion depends on the directional plasticity parameters α and β which are in turn functions of λI. Thus, the level of matrix stress required to trigger the rupture criterion changes with the degree of fiber alignedness (as quantified by the largest eigenvalue of the fiber orientation tensor).
The images below show the results of fitting the multiscale material model to sets of 0°, 90°, and 45° tensile test data for three different short fiber filled injection molded plastics. Collectively, these three materials exhibit a wide range of stiffnesses, plastic response characteristics, and strengths. For each of the three materials, the model is able to closely match the plastic response and the rupture load for all three load orientations (0°, 90°, and 45°).