Determine Initial Fracture Energy Values

Determine the energy dissipated in the composite material.

To use the energy-based degradation (EBD) feature in Simulation Composite Analysis, two values are required:

1. G^m - the total energy dissipated in the composite after a matrix failure (user material constant 12)
2. G^f - the total energy dissipated in the composite after a fiber failure (user material constant 14)

The EBD feature in Simulation Composite Analysis uses a linear degradation model as depicted below.

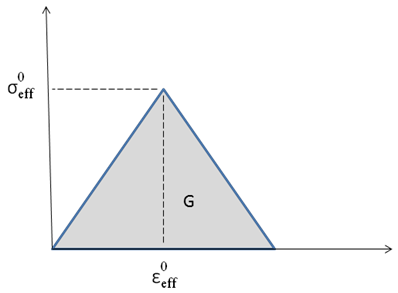
From the image above, the total energy of an element can be expressed as

where 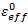is the value of the composite effective strain at matrix/fiber failure, 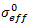is the effective stress of the composite at matrix/fiber failure, and V_e is the volume of the element.

For the matrix constituent, is expressed as,

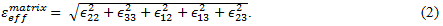
For the fiber constituent, 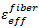is expressed as,

The effective stress of the matrix constituent, 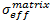, is similarly expressed as,

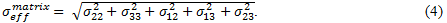
The effective stress of the fiber constituent, 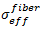, is similarly expressed as,

In Equations 2-5, the 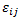and 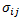values are all composite lamina strains and stresses. To estimate the energy dissipated at failure, the composite lamina strain and stress values can be replaced with the failure strain and failure stress values. The following strength (failure stress) values are available for IM7/8552:

1. ⁺S₁₁ = 362 ksi
2. ⁺S₂₂ = ⁺S₃₃ = 9.29 ksi
3. S₁₂ = S₁₃ = 13.2 ksi
4. S₂₃ = 13.8 ksi

If there are no available failure strain values, simplified Hooke's law can be used to determine failure strain assuming the material response prior to failure is approximately linear,

The following elastic moduli (E) are available for IM7/8552:

1. E₁₁ = 20 Msi
2. E₂₂ = E₃₃ = 1.42 Msi
3. G₁₂ = G₁₃ = 0.669 Msi
4. G₂₃ = 0.0475 Msi

Using the material properties provided for IM7/8552 and substituting Equation 6 into Equations 2 and 3, the following effective strain and stress values at failure for IM7/8552 can be calculated:

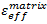1. = 0.0413
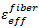2. = 0.0181
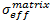3. = 26.7 ksi
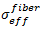4. = 362 ksi

This example problem was constructed using 2D shell elements, which do not have an element volume. This value can be estimated by multiplying the element area by the laminate thickness. The element area can quickly be determined by squaring the global seed size of the mesh assigned to the finite element model. In this example, a global seed size of 0.05 in. was assigned to the OHT model. The laminate used for the OHT is a 16 ply laminate with a ply thickness of 0.0072 in. Using these values, an element volume of 0.0115 in.³ is calculated.

Entering the element volume, effective strain/stress for the matrix, and effective strain/stress for the fiber into Equation 1 results in the following energy values:

• G^m = 12.7 in.-lb.
• G^f = 75.5 in.-lb.

It is these two values that will be entered for user material constants 12 and 14 when using Energy-Based Degradation.