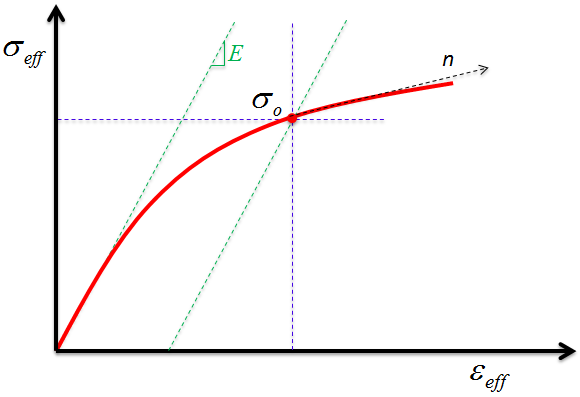
The response of the matrix constituent material is provided by a Ramberg-Osgood plasticity model [13] that has been enhanced to allow the predicted plastic response to exhibit sensitivity to the direction of the loading relative to the fiber direction. The effective hardened yield strength of the matrix constituent material can be expressed as

where σ0 and n are the typical material parameters used by the standard (isotropic) Ramberg-Osgood plasticity model, and εp,eff is the effective plastic strain in the matrix constituent material. The yield function is satisfied when the effective stress in the matrix constituent matches the hardened yield strength.

For isotropic materials, the effective (scalar) stress is often represented by the von Mises stress
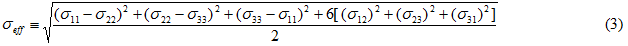
where it is understood that the stress components represent the average stress in the matrix constituent material. Similar to the effective hardened yield strength, the effective stress is also a function of the effective plastic strain εp,eff in that the instantaneous tangent modulus Etan of the matrix constituent material is required to compute the stress components, and Etan is dependent on the effective plastic strain εp,eff as shown in the equation below.

In Eq. 4, H is the plastic modulus of the matrix constituent material and is expressed in terms of εp,eff as follows.

Thus, the determination of the plastic evolution that occurs during an imposed total strain increment reduces to finding the value of εp,eff that allows the material state to remain on the expanding yield surface; i.e. we iteratively solve Eq. 2 for εp,eff.
The Ramberg-Osgood model (Eqs. 1-5) predicts a plasticity response that is isotropic. However, for short fiber filled plastics that have a high degree of fiber alignment, the degree of plasticity exhibited prior to final rupture will depend strongly upon the direction of the loading relative to the average direction of the reinforcing fibers. The Ramberg-Osgood model can easily be enhanced to accommodate directional dependency. To do so, we simply modify the form of the effective stress (Eq. 3). In the present model, the modified effective stress is expressed as

where α and β are weighting coefficients used to differentiate the impact of stress components in the average fiber direction compared to stress components that are normal to the average fiber direction. In this directionally dependent formulation, the plasticity parameters that define the material response are σ0, n, α, and β.
It should be emphasized that the material only exhibits strong directional dependency when the degree of fiber alignedness is relatively high. When the fibers are randomly oriented, the plasticity response must revert to an isotropic response. To accommodate these behavioral characteristics, the directionally dependent weighting coefficients (α, β) cannot be constants. Rather, they must be functions of the degree of fiber alignedness. In the present model, α and β are assumed to be linear functions of the degree of fiber alignedness which is quantified by the largest eigenvalue λI of the fiber orientation tensor.

In Eqs. 7 and 8, αm and βm are the values of α and β respectively that are optimized to fit the response characteristics of a strongly aligned material that has a largest fiber orientation eigenvalue of λm,I. θ is the value that both α and β should achieve when the fiber orientation becomes random. Note that λI ranges from 1.0 for a perfectly aligned material to 1/3 for a material with completely random fiber orientation in all three directions (a completely isotropic condition).
However, the condition of a truly 3-D random distribution of fibers is not likely to occur for thin injection molded parts. It is much more likely that a thin injection molded part might contain some locations that exhibit random fiber orientation in the plane of the injection molded part, but not in the part's thickness direction (i.e., λI = 1/2). In order to accommodate this more common form of isotropy, Eqs. 7 and 8 contain the coefficient (λI - 1/2) which ensures that when λI = 1/2, α and β each achieve the same value of θ, and thus the material becomes isotropic.