Drawing the Tiles within the Garden Path

The drawtiles and drow subroutines are used to draw and calculate the circular tiles for the path.

Drawing a Row of Circular Tiles

The circular tiles are drawn at a given distance along the path specified by its first argument and the row is offset perpendicular to the path by a distance specified by its second argument. Each circular tile is drawn within the outline of the garden path based on the values obtained with the gpuser subroutine and stored in the global variables defined earlier. As each row of tiles is drawn, each successive row that is drawn is offset to cover more space and make a more pleasing arrangement.

1. In the Code window, click after the End Sub statement of the drawout subroutine and press Enter twice.
2. Type the following code:

   ' Place one row of tiles the given distance along path
   ' and possibly offset it
   Private Sub drow(pd As Double, offset As Double)
     Dim pfirst(0 To 2) As Double
     Dim pctile(0 To 2) As Double
     Dim pltile(0 To 2) As Double
     Dim cir As AcadCircle
   
     Dim varRet As Variant
     varRet = ThisDrawing.Utility.PolarPoint(sp, pangle, pd)
     pfirst(0) = varRet(0)
     pfirst(1) = varRet(1)
     pfirst(2) = varRet(2)
   
     varRet = ThisDrawing.Utility.PolarPoint(pfirst, angp90, offset)
     pctile(0) = varRet(0)
     pctile(1) = varRet(1)
     pctile(2) = varRet(2)
   
     pltile(0) = pctile(0)
     pltile(1) = pctile(1)
     pltile(2) = pctile(2)
   
     Do While distance(pfirst, pltile) < (hwidth - trad)
       Set cir = ThisDrawing.ModelSpace.AddCircle(pltile, trad)
       varRet = ThisDrawing.Utility.PolarPoint(pltile, angp90, (tspac + trad + trad))
       pltile(0) = varRet(0)
       pltile(1) = varRet(1)
       pltile(2) = varRet(2)
     Loop
   
     varRet = ThisDrawing.Utility.PolarPoint(pctile, angm90, tspac + trad + trad)
     pltile(0) = varRet(0)
     pltile(1) = varRet(1)
     pltile(2) = varRet(2)
   
     Do While distance(pfirst, pltile) < (hwidth - trad)
       Set cir = ThisDrawing.ModelSpace.AddCircle(pltile, trad)
       varRet = ThisDrawing.Utility.PolarPoint( _
       pltile, angm90, (tspac + trad + trad))
       pltile(0) = varRet(0)
       pltile(1) = varRet(1)
       pltile(2) = varRet(2)
     Loop
   End Sub

3. Save the project.

Calculating the Rows of Circular Tiles

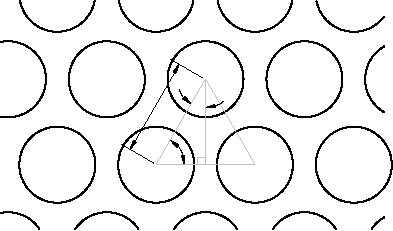
The drow subroutine draws only a single row of circular tiles, but can be used with a While loop to repeatedly draw all the circular tile rows. Tiles in adjacent rows form equilateral triangles, as shown in the previous illustration. The edges of these triangles are equal to twice the tile radius plus the spacing between the tiles. Therefore, by trigonometry, the distance along the path between rows is the sine of 60 degrees multiplied by this quantity, and the offset for odd rows is the cosine of 60 degrees multiplied by this quantity.

An If statement is used to force the offsetting of every other row. If the offset variable is equal to 0, set it to the spacing between the centers of tiles multiplied by the cosine of 60 degrees, as explained earlier. If the offset variable is not equal to 0, set it to 0. This alternates the offset on the rows as you want.

1. In the Code window, click after the End Sub statement of the drow subroutine and press Enter twice.
2. Type the following code:

   ' Draw the rows of tiles
   Private Sub drawtiles()
     Dim pdist As Double
     Dim offset As Double
     pdist = trad + tspac
     offset = 0
   
     Do While pdist <= (plength - trad)
       drow pdist, offset
       pdist = pdist + ((tspac + trad + trad) * Sin(dtr(60)))
   
       If offset = 0 Then
         offset = (tspac + trad + trad) * Cos(dtr(60))
       Else
         offset = 0
       End If
     Loop
   End Sub

3. Save the project.