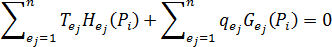Cool is a true 3D mold cooling analysis product. It uses a numerical method developed from BEM (Boundary Element Method). From a physical point of view, BEM treats all boundaries as heat sources (gain / loss heat) during the solution.
The temperature in the mold is determined by combining the influence from all sources.
The equilibrium temperature field of a 3D mold can be represented by Laplace's equation: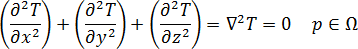
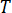 is the temperature
is the temperature 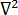 is the Laplace operator
is the Laplace operator 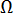 represents the surface area and the inside of the mold
represents the surface area and the inside of the mold
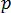 , with boundary conditions unified as:
, with boundary conditions unified as: 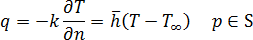
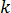 is the thermal conductivity of the mold material
is the thermal conductivity of the mold material 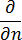 denotes the outward normal derivative on the mold boundary,
denotes the outward normal derivative on the mold boundary, 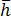 is the equivalent heat transfer coefficient on the mold boundary,
is the equivalent heat transfer coefficient on the mold boundary, 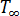 is the equivalent temperature of the ambient environment,
is the equivalent temperature of the ambient environment, 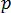 represents a specific point, and
represents a specific point, and 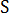 is the mold surface (boundary)
is the mold surface (boundary)
To understand how BEM applies all boundary conditions to the solution of the mold temperature field, let us start with the weighted residual expression: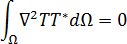
Where 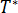 is the weighting function.
is the weighting function.
By making use of Green's second identity, equation 3 can be transformed into the following form: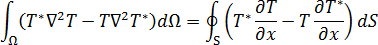
Choosing 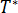 as the fundamental solution of equation 1 defined by:
as the fundamental solution of equation 1 defined by: 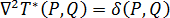
where 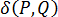 is a Dirac delta function. For a 3D mold, this can be described as:
is a Dirac delta function. For a 3D mold, this can be described as: 
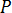 and
and 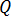 are two points in the space, and
are two points in the space, and 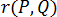 represents the distance between the two points,
represents the distance between the two points,
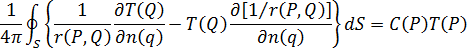
 , and
, and  is a constant in proportion to the interior solid angle.
is a constant in proportion to the interior solid angle.
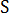 , into
, into  elements, and assume the temperature and temperature gradient are constant over each boundary element, then equation 7 can be discretised into the following form:
elements, and assume the temperature and temperature gradient are constant over each boundary element, then equation 7 can be discretised into the following form:
where
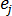 is a specific element
is a specific element 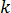 is the thermal conductivity of the mold material
is the thermal conductivity of the mold material 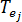 is the temperature of element
is the temperature of element 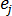
The temperature influence term (or so-called H term), which represents the influence strength of temperature on element 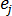 to point
to point 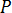 , is given by the expression
, is given by the expression
The heat flux influence term (or so-called G term), which represents the influence strength of heat flux input on element 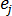 to point
to point 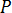 , is given by the expression
, is given by the expression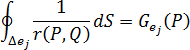
Suppose 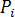 is the centroid of element
is the centroid of element 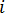 . If we substitute
. If we substitute 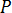 in equation 9 with
in equation 9 with 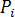 , then we can get
, then we can get  linear equations as:
linear equations as: