Numerical prediction of three-dimensional fiber orientation during mold filling is based on an equation of motion for rigid particles in a fluid suspension.
The analysis consists of two identifiable terms:
- The hydrodynamic term.
- The interaction term.
The hydrodynamic influence on particle motion is described by Jeffery's equation assuming infinite aspect ratio. This theory strictly applies to dilute suspensions but has been shown to provide useful qualitative agreement with experimental data.
The interaction term has been proposed by Folgar and Tucker and is incorporated to model the randomizing effect of mechanical interactions between fibers. It has the form of a diffusion term with the frequency of interaction being proportional to the magnitude of the strain rate. The effect of the interaction term is to reduce highly aligned orientation states predicted by Jeffery's model for some flow conditions, providing improved agreement with experimental observations.
Definition and prediction of fiber orientation
Calculation of three dimensional fiber orientation is performed concurrent with the mold filling analysis on the same finite element mesh. Each triangular element may be considered as consisting of several layers subdividing the local molding thickness. Each layer is identified by the grid point through which it passes. The midplane of the molding passes through grid point 1. An orientation solution is calculated at each layer for each element in the mesh. In this way it is possible to observe the variation in orientation distribution on a set of planes parallel to the mold surface through the cross-section of the molding.
The three-dimensional orientation solution for each element is described by a second order tensor. For graphical representation, the eigenvalues and eigenvectors of the orientation tensor are generated. The eigenvectors indicate the principal directions of fiber alignment and the eigenvalues give the statistical proportions (0 to 1) of fibers aligned with respect to those directions. This information is used to define an orientation ellipsoid which fully describes the alignment distribution of fibers for each element. A general orientation ellipsoid is shown in the figure below.
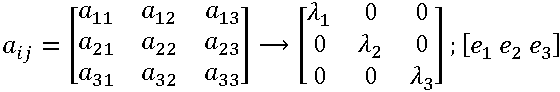
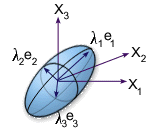
For display purposes, this 3D ellipsoid is projected onto the plane of each element to produce a plane ellipse. This creates a useful representation of orientation distribution, since the gapwise orientation components eliminated by projection are usually small. In this representation a near random distribution is displayed as an ellipse tending to a circle while, for a highly aligned distribution, the ellipse degenerates to a line.
Description of the orientation tensor
The second order orientation tensor,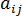 
, provides an efficient description of fiber orientation in injection moldings. The tensor has nine components, with the suffixes for the tensor terms being:
- In the flow direction.
- Transverse to the flow direction.
- In the thickness direction.
Typically these axes apply:
- The X-Y (or 1-2) flow plane.
- The Z-axis in the thickness direction, out of the 1-2 flow plane.
The original nine components reduce to five independent components, due to:
- Tensor symmetry
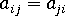, and - A normalization condition
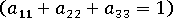
These three major orientation components have been included in the orientation considerations:
-
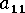, fiber orientation in the flow direction, varying from 0 to 1.0. -
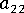, fiber orientation transverse to flow, varying from 0 to 1.0. -
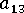, tilt of orientation in the 1-3 plane, varying from -0.5 to 0.5.
Note: The flow direction orientation term, 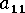, contains most of the quantitative information about the microstructure and is most sensitive to flow, processing and material changes.
A fiber orientation model
A composite material of interest may be considered as particles or fibers suspended within a viscous medium. There may be mechanical and/or hydrodynamic interactions between the fibers.
The suspension may be dilute, semi-concentrated or concentrated, as discussed below:
-
A dilute suspension is one in which the fibers are never close to one another and do not interact.
-
A semi-concentrated suspension would have no mechanical contact between the fibers, but the hydrodynamic interactions become significant.
-
In a concentrated suspension, the fiber orientation behavior becomes very complex, since both mechanical and hydrodynamic fiber interactions apply.
Jeffery first modeled the motion of a single fiber immersed in a large body of incompressible Newtonian fluid. Jeffery's model applies only to suspensions that are so dilute that any inter-fiber interactions (even hydrodynamic interactions) are negligible.
An important measure for assessing suspension concentration is the average distance between the fibers.
Considering fibers of diameter (d) and length (L), with an aspect ratio (L/d), a fiber concentration by volume (c) (or volume fraction ) and having a uniform length distribution, a typical concentration classification scale is:
- Dilutec << (d/L)2.
- Semi-concentrated (d/L)2 < c < (d/L).
- Concentrated c > d/L.
For example, if L/d is 10 (a small value for reinforcing fibers in a composite), then the fiber concentration must be much less than 1% by volume for Jeffery's equation to apply.
For commercial materials, the fiber aspect ratio L/d is often 20 or more, so the values for the above concentrations are:
- Dilute, c << 0.025.
- Semi-concentrated, 0.0025 < c < 0.05.
- Concentrated, c > 0.05
These classification scale cutoffs would typically translate to about 0.5% and 10% by weight.
Most commercial composites contain 10% to 50% fibers by weight, which can be regarded as being concentrated suspensions.
For semi-concentrated suspensions, a model has been proposed by Dinh and Armstrong. The orientation of the fiber follows the bulk deformation of the fluid with the exception that the particle cannot stretch.
For concentrated suspensions, a term, called "the interaction coefficient" (or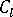 
), has been incorporated in the phenomenological model for fiber orientation proposed by Folgar and Tucker:
- Interactions among fibers tend to randomize the orientation.
- The term takes the same form as a diffusion term and since interactions only occur when the suspension is deforming, the effective diffusivity is proportional to the strain rate.
- The dimensionless 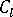term determines the strength of the diffusion term.
Adding the rotary diffusion term to account for the fiber interactions has been found to improve the orientation predictions, since Jeffery's equation alone does not give qualitatively accurate predictions for fiber orientation.
Until now, the Folgar-Tucker model has been the best available for fiber orientation modeling in concentrated suspensions. The model has been given in this form by Advani and Tucker:
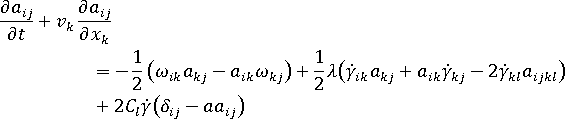
where:
-
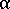equals 3 for 3D and 2 for planar (2D) orientation -
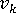is the velocity component -
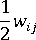is the vorticity tensor, and 
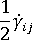is the deformation rate tensor. -
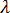is a constant that depends on the geometry of the particle -
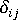is a unit tensor - 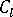is the interaction coefficient
Fiber orientation model closure
The tensor form of the fiber orientation model from Advani and Tucker is not yet a suitable derivative for a second order orientation tensor, because it contains the fourth order tensor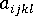 
.
The derivative for a fourth order tensor contains a sixth order orientation tensor and so on. The only way to develop a suitable derivative is to approximate the fourth order tensor in terms of a second order tensor.
This approximation is called a "closure approximation". Various approximations have been tested by Advani and Tucker. However, the presence of the approximation itself may introduce some error into the simulation results. So the closure approximation is the most challenging problem associated with this model. No value of 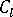can make the fiber orientation model expression fit all the orientation model components.
Examination of the Advani and Tucker fiber orientation model form indicates two ways to control the fiber orientation prediction accuracy:
-
Find a more accurate closure.
-
Find a new interaction model that considers the closure error.
While the first method would be preferred, no closure has been found to satisfactorily cover the range of shearing and stretching flows for a multi-decade range of .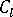
The effect of the closure approximation is to predict too much out-of-plane orientation. This result has been addressed by the fiber orientation model form proposed by Autodesk.