The option to perform a crystallization analysis when using a thermoplastic, semi-crystalline material with appropriate crystallization morphology properties data has been implemented.
Crystallization kinetics modeling
The modeling of the crystallization kinetics, including flow enhanced crystallization, and the flow-induced morphological changes of semi-crystalline materials during and after shearing flow have been implemented in the thermoplastic flow solvers.
The crystal growth rate was not seen to be strongly influenced by material flow. Therefore, it is assumed that the growth rate depends only on temperature and follows the Hoffman-Lauritzen theory[1]: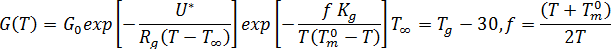 
where 
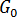and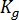 
are material grade-specific constants which can be determined under quiescent conditions, 
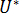is the activation energy of motion, 
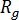is the gas constant, 
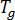is the glass transition temperature, and 
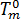is the material grade-specific equilibrium melting temperature which is assumed to depend on pressure only.
A linear function[2] is chosen to describe the pressure dependence[2]: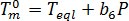 
where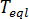 
is the equilibrium melting temperature, 
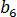is a grade-specific constant of the PVT model for the material, and P is the pressure.
Nucleus generation is expressed as the sum of the number of activated nuclei in the quiescent condition,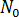 
, and the number of activated nuclei induced by the flow, 
: 
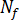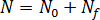
The number of activated nuclei in the quiescent condition is assumed to be a unique function of the supercooling temperature,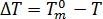 
, and is described by[3]: 
where 
and 
are material grade-specific constants.
The effect of flow on crystallization is considered by relating excess free energy and flow-induced orientation to crystallization kinetics. The number of flow-induced nuclei is given by the following differential equation: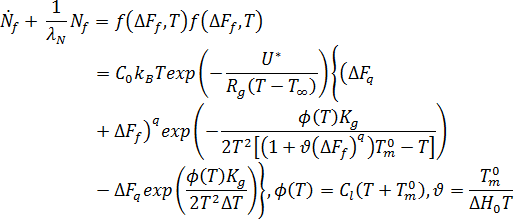 
Crystallinity development leads to an increase in viscosity and, eventually, to solidification. An enhancement factor was adopted in the simulation to describe the effect of crystallinity upon viscosity[4]: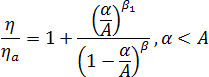 
where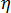 
is the viscosity of the whole system, 
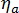is the viscosity of the amorphous phase, and 
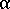is the relative crystallinity.
References
[1] Lauritzen, S. I., and J. D. Hoffman, ''Theory of formation of polymer crystals with folded chains in dilute solution,'' J. Res. Natl. Bur. Stand. 64A, 73-102 (1960)
[2] Fulchiron, R., E. Koscher, G. Poutot, D. Delaunay, and G. Regnier, ''Analysis of the pressure effect on the crystallization kinetics: dilatometric measurements and thermal gradient modelling,'' J. Macromol. Sci., Phys. 40, 297-314 (2001)
[3] Koschei, E., and R. Fulchiron, ''Influence of shear on polypropylene crystallization: morphology development and kinetics,'' Polymer 43, 6931-6942 (2002)
[4] Zheng, R. and P. K. Kennedy, "A model for post-flow induced crystallization: General equations and predictions", J. Rheol., 48(4), 823-842 (2004)