Iterative Solver Parameters - General Information

The iterative solver application is recommended for solving large-scale (15,000 - 1,000,000 equations) linear static tasks and eigenvalue problems (modal or buckling analysis). Traditional direct methods (frontal, skyline, sparse) are very time-consuming and require large amounts of disk space to store a factorized matrix. Such an approach may prove very efficient for the analysis of structures containing solid FE. Solvers of this type may be very useful during linear static analysis (searching for optimal design parameters, for example), when it is possible to obtain approximate solutions for a small number of load cases. The element-by-element control of data correctness of Vinget regularization (as shown below) constitutes an additional application of iterative solver which enables you to detect difficulties finding errors in the FE model.

The preconditioned gradient method (PCG), including several types of preconditioning, is currently implemented.

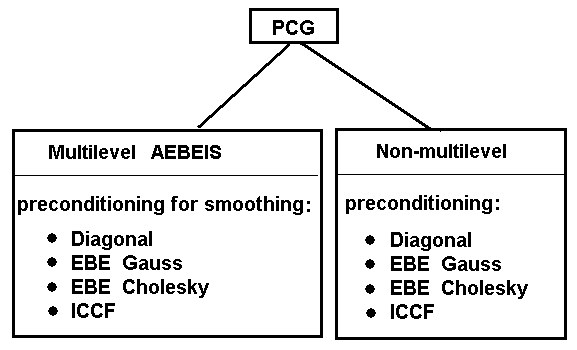
AEBEIS: Aggregation Element-by-Element Iterative Solver ^1,2
EBE: Element-by-Element
ICCF: Incomplete Cholesky Factorization approach

AEBEIS is a multi-level, aggregation, element-by-element iterative solver that combines the advantages of quick iterative methods with the inexpensive EBE technique. It allows acceleration of basic operations by means of the inexpensive method with respect to memory requirements. Aggregation methods such as this allow analysis of solids and shells (just as multi-grid methods do), as well as bars and combination structures from bars, shells, and solids.

AEBEIS typically provides quicker convergence compared to non-multilevel methods. It is restricted only to 3D structures and 2D frames. AEBEIS shows a reduced sensitivity to ill-conditioned problems of appropriate non-multilevel iterative methods, but it is less safe. In rare cases a "lock" of preconditioning takes place, whereas the convergence is still slow.

AEBEIS enables the application of 2D and 3D bar elements, shell elements (3, 4, 6, and 8 node elements), solid elements. It also enables additional structure component elements such as elastic supports, offsets, releases, and rigid links. There are no restrictions concerning element or structure types for a non-multilevel method.

The following types of preconditioning are available in both AEBEIS and non-multilevel methods.

Diagonal - Jacobi preconditioning (apply only in well-conditioned problems).
EBE Gauss - modified EBE Gauss-Seidel-Cholesky preconditioning ^1,2.
EBE Cholesky - EBE Cholesky preconditioning ^1,4.
ICCF - incomplete Cholesky factorization approach ^5,6.

The ICCF approach is quicker than other methods (Diagonal, EBE Gauss, EBE Cholesky) and uses approximately the same number of iterations to obtain convergence, such as the EBE Gauss or EBE Cholesky methods. It does not use the I/O operations of the disk but maintains higher RAM requirements. ICCF is preferred if the computer has a sufficient amount of RAM for the task. RAM and disk requirements of EBE Gauss and EBE Cholesky methods are minimal, but they are slower than the ICCF approach.

References

Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.
Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26-27, 1987.
Hughes T.J.R., R.M.Ferencz, and j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61.
S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148 , p.75-104.
M.Papadrakakis, Solving large - scale problems in mechanics, John Wiley & Sons Ltd., 1993.