How to Calculate Pm and Pb

This page discusses how the primary membrane and primary bending stresses (P_m and P_b) are calculated.

Note: The primary bending stress (P_b) is not output or listed directly within the Stress Linearization interface. Rather, the sum of the primary membrane and primary bending stresses (P_m + P_b) is output, along with the primary membrane stress alone (P_m).

The calculation of these stresses involves several steps. We begin by integrating the six stress tensors, σ_N, σ_T, σ_H, τ_NT, τ_TH, τ_NH, along SCL to obtain the total load (F_N, F_T, F_H, F_NT, F_TH, F_HN) using:

Where T is the location along the SCL.

Then, we calculate the membrane stress (F/A) for all 6 components. For an SCL of length t,

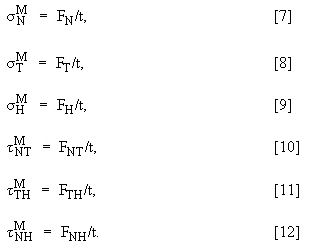
The principal membrane stresses () are obtained from the tensor whose components are given by equations 7 through 12. These stresses are obtained by recasting this tensor in the principal axis direction.

Next we develop the bending stresses by subtracting the membrane stress from the total stress distribution. This is done stress point by stress point. We only need to consider the two component stresses perpendicular to the SCL (nominally the hoop and meridional component stresses). First, we develop the moment-load distribution for an SCL of length t. Then we integrate the moment load-distribution to obtain the moment on the cross section.

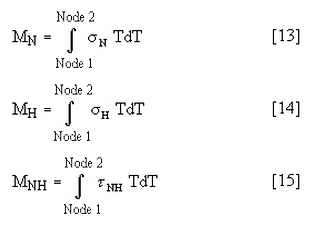
Again, these integrals should be calculated using trapezoidal integration. The subsequent results are used to calculate the bending stress (Mc/I) for an SCL of length t from:

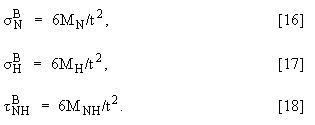
The next step is to calculate the principal stress at each end of the SCL (). These principal membrane plus bending stresses are obtained from the tensor whose components are obtained by substituting T=Node 1 and T=Node 2

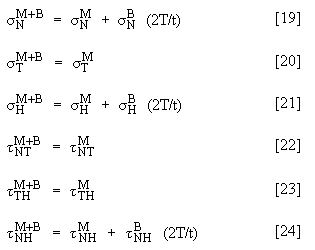
The membrane stresses are obtained from equations 7 through 12, and the bending stress from equations 16 through 18. Again, note how one gets two sets of principal stresses: one at T=Node 1 and another at T=Node 2. Again, the principal stresses are obtained by recasting the tensor in the principal axis direction.

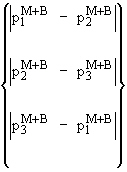
At this point we have all the principal membrane stresses,

and the sum of the principal membrane and bending stresses,

These values are required to determine the two output scalar quantities:

P_m and
P_m + P_b

according to the following two equations:

P_m = Largest of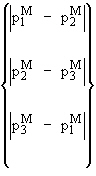

[25]

Pm + Pb = Largest of

[26]

Note how equation 26 must be evaluated twice because there exists two sets of values: one at T=Node 1 and another at T=Node 2. The output quantity should be that of the evaluation that resulted in the largest value.

Reference: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev 4, 2000.