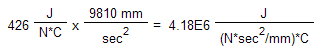Convert Mass Units

Autodesk Simulation requires the Model Units to be in a consistent set of units. For example, to get the force applied to an element due to a pressure load, the processor calculates F=PxA without considering the units. Therefore, the units of force and length used for the pressure input and the units of length for the geometry of the mesh (which results in an area) must be consistent.

Furthermore, any system of units is based on primary (or base) dimensions and secondary (or derived) dimensions. The following table shows two common base and secondary dimensions. In the Model Units, force, length, and time are the primary dimensions, and mass is a derived dimension.

  SI Units U.S. Customary Units and Autodesk Simulation
Primary Mass Force
Primary Length Length
Primary Time Time
Derived Force Mass

The confusion that this may cause in regards to mass is easily understood if you keep Newton's second law in mind: F = ma.

Tip: The discussion on this page is most relevant to the Model Units where the above units must be consistent. The Display Units do not need to be dimensionally consistent. By choosing the right Display Units, the confusion with converting the mass density (and instructions on this page) can be avoided (see Select a Units System).

Convert mass units

Mass density is best illustrated by Newton’s second law,

weight = mass*g

mass = weight/g

Dividing both sides by the volume gives

mass density = weight density/g

As an example, the mass density of Structural Steel (ASTM-A36) with a weight density (or specific weight) of 0.284 lbf/in 3 is calculated as follows: 

mass density = (0.284 lbf/in 3 ) / (386.4 in/sec 2 ) = 7.35E-4(lbf*sec 2 /in)/in 3

where the term (lbf*sec 2 /in) is the mass, and /in 3 gives the density. 7.35E-4 is entered as the mass density in the material properties.

Another example of the proper conversion to mass units is the specific heat. The specific heat of Aluminum 2024 is 0.22 BTU/(lbm*F). The conversion procedure to mass units when using Model Units is as follows:

0.22 BTU/(lbm*F) = 0.22 BTU/(lbf*F)

To convert to consistent mass units, divide the weight by gravity. Since the weight term is in the denominator, dividing weight by gravity results in the gravity term in the numerator:

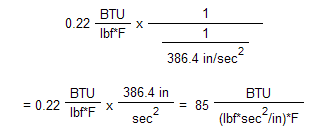
where again the term lbf*sec 2 /in represents the mass. 85 is entered as the specific heat in the material properties. You should be able to confirm, dimensionally at least, that specific heat times mass will result in the correct value:

Note: The above calculations make use of the fact that one lbf equals one lbm at standard gravity. Thus, lbm is not recognized as a mass unit for Model Units. The Display Units do include the unit lbm, so the input can be simplified in many cases by creating a Display Unit that uses lbm.

Similar conversions are required with metric units when the Model Units are changed from the base of Newton, meter, second, kilogram. For example, the specific heat of water is about 4180 J/(kg*C). If the units of length in the model are millimeters, the Model Units of mass are derived based on Newton, millimeter, and second. Thus, the mass in kilograms first needs to be converted to a weight, and then converted to consistent mass units.

Convert provided mass to weight units (remember, the model is using Newtons):

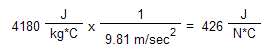
Divide the weight by gravity to get the model (consistent) mass units. Since the weight term is in the denominator, dividing weight by gravity results in the gravity term in the numerator (remember the model is using mm for length):

4.18E6 is entered as the specific heat in the material properties.

Parent topic: Units Systems