Overview:
The damage model simulates the damage onset and the progressive growth for elastic-brittle orthotropic materials, such as a composite. The model is primarily intended to be used to simulate fiber-reinforced composite materials. The damage model describes three phases of the material's response:
- the undamaged material response, which must be linear elastic
- the damage initiation
- and the progressive damage growth.
In the model, the damage in materials is characterized by the degradation of the material stiffness. The fibers of the composites are assumed to be parallel and in the element's material axis 1 direction. Four different failure modes are considered:
- fiber rupture in tension;
- fiber buckling and kinking in compression;
- matrix cracking in transverse tension and shearing;
- matrix crushing in transverse compression and shearing.
The material behavior is defined as σ = Cdε, where Cd is the elastic matrix that reflects the damage and is calculated as follows:
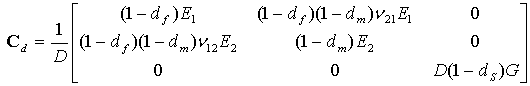
where
- D=1-(1-df)(1-dm)ν21ν12ν
- df represents the fiber damage
- dm represents the matrix damage
- ds represents the shear damage
- E1 is the Young's modulus in the fiber direction
- E2 is the Young's modulus in the direction perpendicular to fibers
- G is the shear modulus
- ν21 and ν12 are Poisson’s ratios.
Damage Initiation:
Damage initiation criteria consider fours different damage modes and have the following forms:
Mode I: fiber tension ( >= 0) |
|
| Mode II: fiber compression ( < 0) |
|
Mode III: matrix tension ( >= 0) |
|
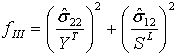
| Mode IV: matrix compression ( < 0) |
|
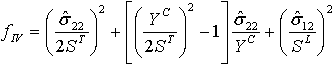
where
- fI, fII, fIII, fIV are the variables associated with the damage initiation criteria. A value of 1.0 or higher indicates that the initiation criterion has been met.
- XT represents the longitudinal tensile strength
- XC represents the longitudinal compressive strength
- YT represents the transverse tensile strength
- YC represents the transverse compressive strength
- SL represents the longitudinal shear strength
- ST represents the transverse shear strength
- α represents the coefficient that determines the contribution of the shear stress to the fiber tensile initiation criterion and 0 <= α <= 1.
, , and
are the components of the effective stress tension,
, which is computed from =Mσ. σ is the nominal stress and M is the damage operator, defined as follows:
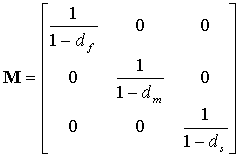
The internal damage variables df, dm, and ds are derived from the damage variables dft, dfc, dmt, and dmc corresponding to the four modes:
df = …
- dft if 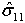>= 0
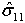- dfc if < 0
dm = …
- dmt if 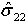>= 0
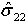- dmc if < 0
ds = 1-(1-dft)(1-dfc)(1-dmt)(1-dmc)
The equations for the damage variables dft, dfc, dmt, and dmc are given below.
Damage Evolution:
Based on the damage initiation in the previous section, the evolution of the damage variables are defined here for each mode. To alleviate the mesh dependency during material softening, equivalent stress and displacement are introduced.
Equivalent stresses and displacements are defined for each of four damage modes:
- Fiber tensile mode:
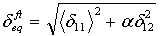
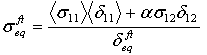
- Fiber compressive mode:
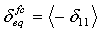
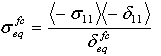
- Matrix tensile mode:
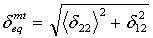
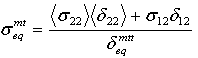
- Matrix compressive mode:
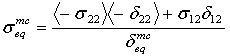
where δij = Lcεij and Lc, the characteristic length, is computed as a square root of integration point area. The operator <x> is the Macauley bracket operator defined as <x> = (x + |x|) / 2.
Based on equivalent stresses and displacements, the damage variable is calculated as:
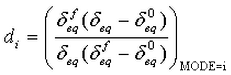
where i corresponds to the four modes I through IV (or dft, dfc, dmt, and dmc). The results are in the range of 0 to 1 where 0 indicates there is no damage and the element can support a full load, and 1 indicates complete damage and the element cannot support any load in the respective direction.
δ0eq and σ0eq are the initial equivalent displacement and stress at which the initiation criterion was met. They are defined as
.
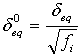
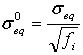δfeq = 2Gci / σ0eq is the equivalent displacement at which the material is completely damaged in this failure mode, where Gci, the energy dissipated due to the failure mode i (either tension or compression), controls the damage evolution.
The maximum size for the finite element for each damage law is Lc <= 2 * EiGci / (Xi)2, where Ei, Gci, and Xi are the Young modulus, fracture energy, and strengths, respectively. Once again, i corresponds to the four damage modes I through IV (or corresponding designation depending on the variable).
Damage Stabilization and Viscous Regularization:
A generalized Duvaut-Lions viscous regularization scheme is introduced to overcome convergence difficulties led by material softening behavior and stiffness degradation in an implicit analysis. In the regularization scheme, a viscous damage variable is defined as
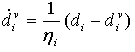
ηi is the viscosity coefficient representing the viscous system relaxation time, and di is the damage variable evaluated in the inviscid backbone model, where i denotes a damage mode (I through IV, or ft, fc, mt, and mc as appropriate to the variable). The regularized damage variable is updated as:
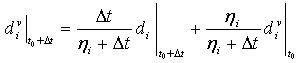
The damaged response of the viscous material is given as σ = Cd(dν)ε. A small viscosity parameter usually helps improve the rate of convergence of the model in softening scheme, without compromising results.
Other: Additional calculations of interest are as follows:
- Complementary free energy density:
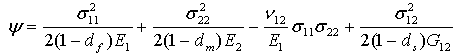
- Damage Energy:
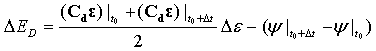
Viscous energy dissipation:
References:
- Hashin, Z., A fatigue failure criterion for fiber reinforced materials, Journal of Composite Materials, 7 (1973), 448-464.
- Lapczyk, I. and Hurtado, J.A., Progressive damage modeling in fiber-reinforced materials, Composites: Part A, 38 (2007), 2333-2341.
- Iannucci, L. and Ankersen, J., An energy based damage model for thin laminated composites, Composites Science and Technology, 66 (2006), 934-951.
- Maimi, P., Camanho, P.P., Mayugo, J.A., and Davila, C.G., A continuum damage model for composite laminates: Part I - constitutive model, Mechanics of Materials, 39 (2007), 897-908.
- Maimi, P., Camanho, P.P., Mayugo, J.A., and Davila, C.G., A continuum damage model for composite laminates: Part II - computational implementation and validation, Mechanics of Materials, 39 (2007), 909-919.