Désignations adoptée:
E - Module de Young
G - Module de cisaillement.
ν - Coefficient de Poisson
fd - Limite d'élasticité
Ax - Section transversale
Ix - Constante de torsion
Iy - Moment d'inertie - flexion dans le plan XZ
Iz - Moment d'inertie - flexion dans le plan YZ
ky; kz - Coefficients de correction de la rigidité au cisaillement dans les directions Y et Z
L - Longueur de barre.
-
Remarques et hypothèses préliminaires
Les hypothèses suivantes ont été adoptées pour les éléments de type barre(poutre) :
- Formulation uniformes pour 2D et 3D (portiques 2D et 3D, grillages)
- Éléments uniformes permettant la non-linéarité matérielle et/ou géométrique
- Degrés de liberté de déplacement standard aux 2 nœuds extrêmes
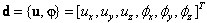
- L'utilisation des opérations suivantes est admise :
- Déformation de cisaillement incluse (modèle de Timoshenko).
- Section transversale conique - uniquement pour la non-linéarité géométrique.
- Fondation de Winkler
- Il existe deux niveaux de non-linéarité géométrique disponibles : non-linéarité (théorie de deuxième ordre) et P-DELTA qui est la théorie la plus précise possible avec les déplacements et les rotations importants ; il s'agit d'une approche incrémentielle avec une mise à jour de la géométrie.
- En supposant de petits déplacements et l'absence de non-linéarité physique de la limite, les résultats sont les mêmes que pour des éléments linéaires standard.
- Dans l'analyse de la non-linéarité matérielle, les modèles calqués et le principe constitutif contrainte/déformation de la contrainte/déformation sur le point (calque) sont appliqués.
- Les états de cisaillement et de torsion sont considérés comme linéairement élastiques et doivent être découplés des forces axiales et des moments fléchissants au niveau transversal.
- Les relâchements et les rotules non linéaires peuvent être définis uniquement comme éléments DSC.
- Tous les types de charge d'éléments sont admissibles (de la même façon que pour les éléments standard). Toutefois, il est supposé que les forces nodales agissant sur une structure sont déterminées au début du processus. Les modifications apportées au transfert de charge sur les nœuds résultant de la non-linéarité géométrique ou matérielle sont ignorés.
- A l'exception de l'élément élasto-plastique, il est également possible de générer des rotules élasto-plastiques dans les sections transversales de barres sélectionnées en tant qu'extension de "rotules non linéaires" (voir le point 5).
-
Géométrie, cinématique et déformation
Géométrie, convention de signe pour les forces, les déplacements, les contraintes et les déformations
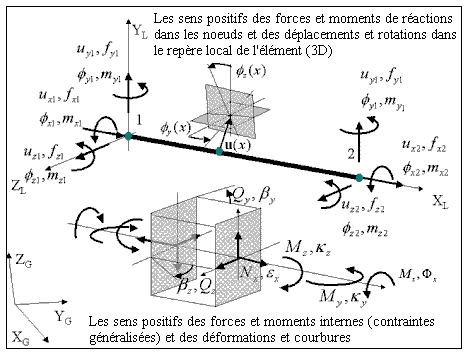
Relations cinématiques de base
Dans le système local de l'élément et dans l'intervalle géométriquement linéaire, les déformations généralisées E au niveau de la section transversale sont les suivantes (le symbole (
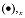indique le calcul du différentiel dans la direction de l'axe de la barre) :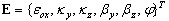 
où :
Déformation axiale de l'axe de la barre :
e0x = u,x
Courbures :
K y = fy'x
K z = - f z'x
Cornières moyennes (déformation) :
b y = n 'x - f z'
b y = w 'x - f y
Cornière de torsion de l'unité :
j = f x'x
Approximation du déplacement
Lorsqu'il est possible de prendre en compte l'influence du cisaillement et la constance des résultats obtenus pour l'élément linéaire, les fonctions de forme physique prenant en compte l'influence du cisaillement ont été mises en œuvre.
Barres 2D :
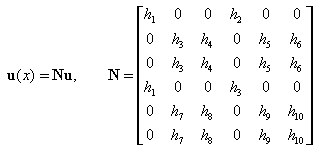
Les fonctions de forme et leurs dérivées sont exprimées par des formules :
où :
x = x / L
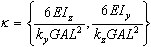pour les plans XY et XZ, respectivement. Relations cinématiques de la notation de matrice (théorie géométriquement linéaire)
Lorsque l'influence des déformations imposées est prise en compte
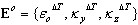
Incrément de déformations: généralisées (coupe)
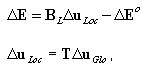
2D :
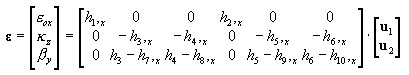
3D :
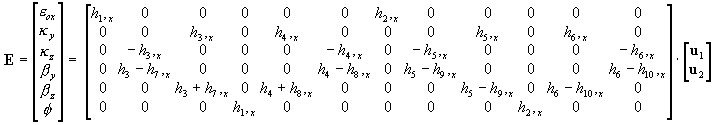
où :
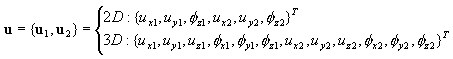
Déformations à un point (calque)
Étant donnée les déformations généralisées {ε 0x, k y , k x } d'une coupe, la déformation e xl ou son incrément De xl à tout point de la coupe l - des coordonnées yl, zl, est calculée en tant que
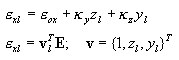
enfin, incrément de déformation dans le calque :
-
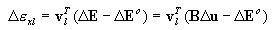
Contraintes et efforts internes dans un élément
Le principe constitutif au niveau du point
Le principe est adopté dans le formulaire incrémentiel général, où les contraintes en cours σx n + 1 sont définies comme une fonction de contrainte pour le dernier équilibre σx n et l'incrément de déformation en cours avec les déformations imposées (thermiques) prises en compte,
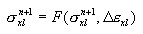
sur la base de la fonction σ = f(ε) qui décrit la relation dans le processus du chargement actif et de la spécification du principe de déchargement et de rechargement. En particulier, il peut s'agir du principe élasto-plastique avec trempe linéaire et le principe spécifié de déchargement, tel que (a) élastique, (b) plastique, (c) avarie, (d) mixte. Pour un déchargement élastique, le processus passif et actif s'effectue le long de la même trajectoire σ = f(ε). Pour les autres, il est effectué le long de la ligne droite déterminée par le point de départ d'un processus donné de déchargement {ε UNL, σ UNL }et le module de déchargement D UNL défini comme
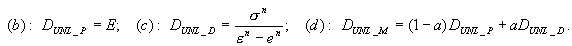
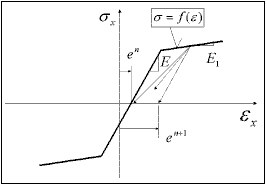
e n est une déformation mémorisée, pour laquelle le processus actif a démarré, commencé après un dépassement de 0 par des contraintes avec le déchargement supposé (e 1 = 0).
Pour l'analyse, il est nécessaire de fournir la rigidité en cours qui est supposée en dériver.
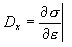
Calcul des efforts et des valeurs de rigidité de coupe
Au niveau de la coupe, le vecteur de efforts internes (résultantes de contrainte) est composé des éléments suivants :
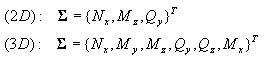
Les états de cisaillement et de torsion ΣST sont considérés comme linéairement élastiques et ne sont pas conjugués avec l'état des efforts axiaux/fléchissants dans la coupe.
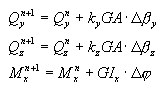
Les états de compression ou de tension Σ Nm sont généralement considérés comme conjugués lors de l'application de l'approche par couche. Cependant, tant que l'état élastique est garanti, c'est-à-dire jusqu'à ce que la déformation généralisée remplisse la condition d'état élastique suivante :
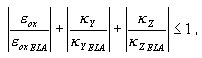
où :
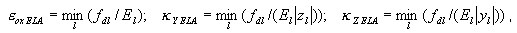
La coupe transversale est considérée comme élastique et l'approche par couche n'est pas activée.
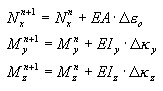
Une fois que la violation de la condition d'état élastique est vérifiée, les contraintes induites par les déformations axiales et de flexion sont calculées séparément pour chaque couche et, sur leur base, les grandeurs sectionnelles sont calculées.
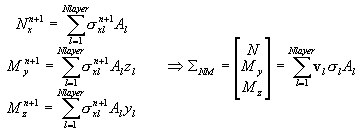
La rigidité au niveau de la coupe transversale est calculée comme suit :
dans l'état élastique :
D = diag {EA, EIy, EIz, KyGA, kzGA, GIx)
après dépassement de la condition d'état élastique :
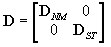
où :
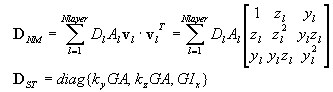
Vecteur de force nodale et matrice de rigidité de l'élément
Ces valeurs sont calculées à l'aide de la formule standard d'application de la quadrature de Gauss (Ngauss=3).
-
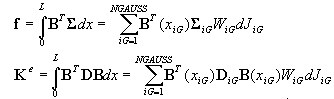
Non-linéarité géométrique
Les configurations suivantes sont prises en compte :
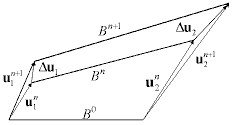
B0 - Configuration initiale
Bn - Configuration de référence (la dernière pour laquelle les conditions d'équilibre sont vérifiées)
Bn + 1 - Configuration courante (itérée).
Un point d'entrée pour la formulation d'éléments est le principe de travail virtuel enregistré dans le formulaire suivant pour les incréments de déplacement :
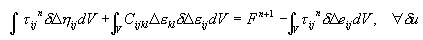
où : l'incrément de déformation Δε pendant le déplacement Bn à Bn + 1, Δe, Δη constituent ses composants, par conséquent : linéaires et non linéaires par rapport à l'incrément de déplacement Δu, tandis que τ est une contrainte relative à la configuration de référence et Cijkl est un tenseur des modules d'élasticité tangentielle.
L'option Non-linéarité
Elle correspond à la formulation non linéaire ou théorie de deuxième ordre. Étant donné que la non-linéarité matérielle est possible, la formulation incrémentielle est introduite (toutefois, sans modification de la géométrie des éléments).
Relations cinématiques
Incréments de déformation dans la notation de la matrice :
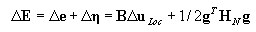
où :
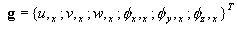
ensuite, le gradient d'incrément de déplacement G = ΓΔu
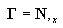
tandis que
est une matrice de sélection.
Vecteur de force nodale et matrice de rigidité de l'élément
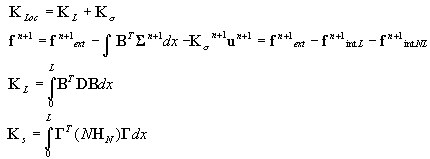
Algorithme au niveau de l’élément
La géométrie de l'élément n'est pas modifiée; la transformation local-global s'effectue en utilisant la matrice de transformation initiale 0 T
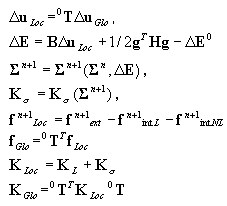
Option P-DELTA
Il s'agit d'une variante de description de barre permettant de grands déplacements. Une approche de la description Lagrange mise à jour est appliquée ici.
Vecteur de force nodale et matrice de rigidité de l'élément
-
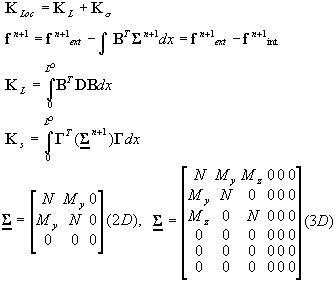
Rotules élasto-plastiques
Vous pouvez également modéliser la construction élasto-plastique d'une structure en introduisant des rotules non linéaires au niveau des coupes transversales de barre sélectionnées. Les caractéristiques d'une rotule représentée par un élément DSC à deux nœuds sont définies en appliquant l'algorithme d'analyse des coupes décrit dans le point 3, en supposant que le rôle des contraintes généralisées e est tenu par des déplacements de nœud mutuels (par rapport aux directions locales des barres) divisés par la longueur adoptée (fictive) de l'élément (ΔL) qui est égale à la hauteur minimale de la coupe. Ils agissent comme volume de l'élément dV=ΔL. Les forces et les déplacements des nœuds nouvellement générés de l'élément DSC constituent les degrés globaux de liberté. En d'autres termes, ils ne sont pas soumis à condensation.
Algorithme au niveau de l’élément-
calcul des contraintes généralisées dans une coupe
-
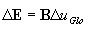
calcul des efforts internes (résultantes de contrainte) et rigidité de la coupe conformément au point 3.2
-
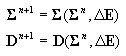
calcul des forces (réactions sur les extrémités des barres) et rigidité de l'élément DSC
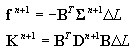
où :
-
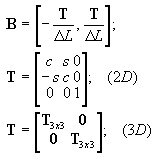