Lors des calculs des dalles orthotropes, la rigidité équivalente est calculée dans chaque point au niveau de la section. Pour un élément de la coque plane en 3D, la rigidité est définie à partir des matrices suivantes :
- matrice de rigidité pour l’état de membrane D
- matrice de rigidité pour la flexion K
- matrice de rigidité pour le cisaillement H.
Si l'on admet que l'orthotropie n'est définie que pour les éléments plans à section symétrique, la définition des matrices mettant en relation la flexion et l'état de membrane n'est pas nécessaire.
Les sections des nervures unidirectionnelles à deux faces, des boîtes de sols unidirectionnelles, des boîtes de sols bidirectionnelles et des grillages constituent des profilés symétriques et l’approche ci-dessus est justifiée. Pour les autres types, ce principe n'est pas satisfait et la solution proposée ne constitue qu'une approximation.
Le plan de référence permettant de définir la rigidité doit être pris plutôt sur le niveau du centre de gravité que sur la ligne centrale (épaisseur de la dalle). Cette approche est plus raisonnable, surtout si l'on prend en compte les vibrations transversales. Du point de vue des calculs de la rigidité, cela n'est qu'une approche, mais elle est plus précise que celle où l'on utiliserait la ligne centrale de l'épaisseur.
La rigidité pour la plaque est définie à partir des matrices suivantes :
- matrice de rigidité pour la flexion K
- matrice de rigidité pour le cisaillement H.
Les valeurs de rigidité relatives aux directions de l'orthotropie sont définies par les matrices générales ci-dessous :
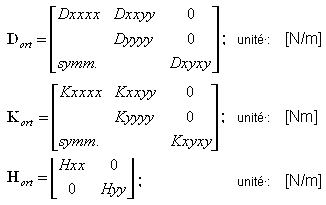
La direction de l'orthotropie X est déterminée par l'utilisateur (définition du vecteur de direction) de la même façon que pour la définition du repère local pour l'affichage des résultats ou du ferraillage V =[vx, vy, vz].
Le vecteur V défini par l'utilisateur génère la direction de l'axe X de l'orthotropie selon le principe :
"La direction X est une direction tangente au plan de l'élément la plus proche de la direction V définie."
Si {e 1 ;e 2 ;e 3 } sont la base locale dans un point donné de l'élément (pour les dalles en 2D, e i coïncide avec les directions des axes XG,YG du repère global), les fonctions trigonométriques sin α ; cos α de l’angle compris entre la direction de l’orthotropie X et l’axe local x1 sont déterminées comme suit :
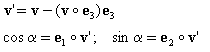
Une fois que les fonctions trigonométriques s = sin α ; c = cos α d'un angle sont déterminées, les matrices de rigidité sont transformées des axes d’orthotropie XY en directions locales de l'élément au moyen des formules suivantes :
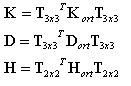
où :
T3x3 est la matrice de transformation pour le tenseur de second ordre en 2D (écrit en tant que matrice 3x3)
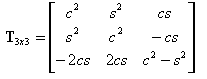
T2x2 étant la matrice représentant la transformation du vecteur 2D
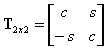
Rubrique connexe :