Les calculs sont similaires aux calculs d’une poutre rectangulaire. Le logiciel calcule les forces dans la poutre et dans les nœuds du panneau (dalle). Les forces sont ensuite réduites au centre de gravité d’une nouvelle section en T.
L’axe passe par le centre de gravité du panneau.
L’approche simplifiée concernant la prise en compte des efforts provenant du panneau consiste à multiplier les efforts dans les nœuds du panneau (communs _4 la poutre) par la largeur efficace d’une dalle associée à une poutre. Pendant le positionnement de la poutre par rapport à la dalle, les excentrements (y compris les excentrements relatifs) sont pris en compte. A la suite de la réduction, il semble que la section en T a été décalée par rapport au plan du panneau d’un excentrement égal à la distance du centre de gravité du centre de la section en T (cf. la figure ci-dessous).
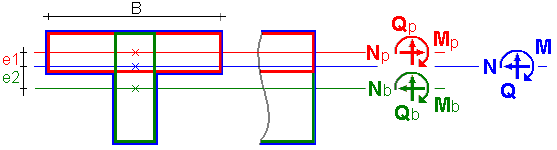
La réduction des efforts au centre de gravité de la section en T est la suivante :
m = Mo + MP * B + NP * b * E1 + Nb * e2
Q = Qb + Qp * B
N = Nb + Np * B
où :
B = beff1+b+beff2
Détermination du centre de gravité de la section en T
Moment statique calculé dans le centre de gravité du panneau (on n’utilise que la poutre et son excentrement)
S = b * h * (décalage)
A = (beff1+b+beff2)*hpl + b*h
Centre de gravité a été décalé par rapport au centre de gravité du panneau :
Z = S/A
où :
b - largeur de la poutre
h - hauteur de la poutre
beff1, beff2 - largeurs efficaces
hpl - hauteur de la poutre (épaisseur du panneau)
offset - excentrement de la poutre par rapport au panneau.
REMARQUES :
- Il convient de noter qu'il peut y avoir des parties communes de la zone du panneau et la poutre ; malheureusement, elles apparaissent deux fois dans les calculs, ce qui aboutit à la croissance de rigidité de la poutre en T. En résultat, les efforts et les flèches sont plus petits
- Les résultats du panneau sont lus sur les nœuds d’éléments finis ; l’affinement du maillage a un effet sur les résultats
- Dans le modèle, l’axe de la section en T est l’axe du centre de gravité du panneau
- A la suite de la simplification, il suffit désormais de multiplier des efforts appropriés dans le panneau par une largeur efficace conventionnelle d’une dalle. En conséquence, les résultats sont estimés.