L'équation de flux de chaleur à l'intérieur du contour illustré ci-dessous peut être présentée comme suit.
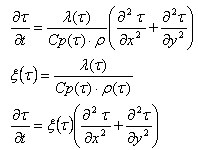
où :
C P - Chaleur spécifique (J/kg * K)
λ - Conductivité thermique (W/m*K)
ρ - Poids volumique (kg/m 3).
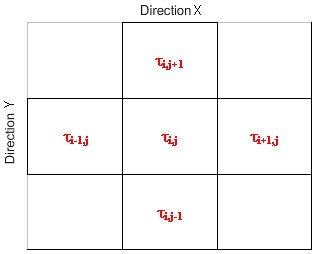
Dans la notation différentielle, les équations de flux de chaleur peuvent être écrites comme suit :
.
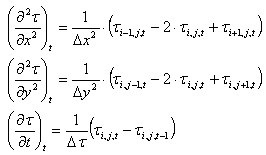Ces équations donnent :
.
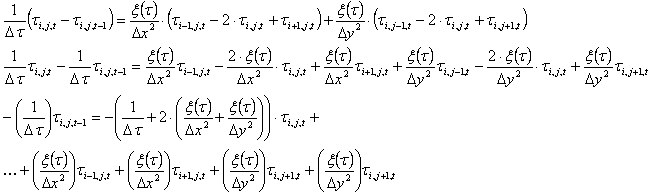Ainsi, pour les nœuds K, le système d'équations M [KxK] x τ [K] = B [K] sera résolu.
Approximations adoptée
Lorsqu'il est nécessaire de connaître la température en cours pour déterminer les coefficients non décrits par des équations, l'approximation des pas temporels précédents est appliquée (différence vers l'avant).
Pour le pas temporel constant Δτ, les résultats suivants sont obtenus :
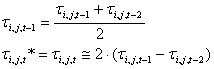
ce qui permet de déterminer :
pour le pas i = 1 t i,j,1 * = t i,j,o.
Conditions aux limites
Des conditions aux limites d'un autre type sont ajoutées à la formulation générale du problème. Elles influent sur les points suivants :
- Convection
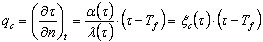
où :
n - Normal par rapport au bord
Tf - Température dans l'environnement extérieur du contour identifiée avec la température d'incendie.
En supposant que le coefficient de convection a est indépendant de la température et en employant les approximations susmentionnées, le résultat obtenu est le suivant :
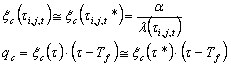. - Radiation
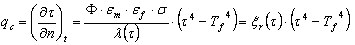
où :
n - Normal par rapport au bord
T f - température dans l'environnement du contour extérieur identifié avec la température d'incendie
Φ - Coefficient de configuration
ε m - Coefficient d'émission de l'élément
ε f - Coefficient d'émission du feu
σ - Constante de Boltzmann 5.65*10 8 (W/m 2 *K 4 ).
En employant les approximations susmentionnées, le résultat obtenu est le suivant :
.
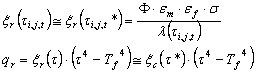Suppositions adoptées pour la norme DTU P 92-701
- Développement d'incendie dans le temps
Incendie décrit sous une forme discrète (tableau) selon la formule suivante :
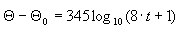(section 4 DTU P 92-701, figure 11) Incendie décrit sous une forme discrète (tableau) selon la formule suivante :
où t est exprimé en [min]
ce qui permet de décrire la température de l'incendie comme suit :
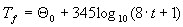
Les valeurs discrètes sont sélectionnées de sorte qu'aucun incrément de température supérieur à 30 % ne puisse s'effectuer dans aucun des incréments temporels. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du développement de l'incendie dans le temps est incluse dans le fichier Fire_DTU.t.
- Conductivité thermique du béton
La dépendance de la conductivité thermique est présentée sous forme tabulaire (section 3.15 DTU P 92-701).
Une description du comportement de la conductivité thermique en fonction de la température est fournie dans le fichier Lambda_DTU.la.
- Poids volumique du béton
Il est indépendant de la température et équivaut à 2 400 [kg/m3].
Une description du comportement du poids volumique selon la température est fournie dans le fichier Ro_DTU.cp.
- Chaleur spécifique du béton
Elle est indépendante de la température et équivaut à 921,096 [J/kg * K], c'est-à-dire 0,22 [kcal/kg * OC] (section 3.16 DTU P 92-701).
Une description du comportement de la chaleur spécifique selon la température est fournie dans le fichier Cp_DTU.cp.
- Coefficient de réduction de la résistance du béton
Le coefficient de réduction de la résistance du béton est présenté sous forme tabulaire (section 3.13 DTU P 92-701).
Une description du comportement de la réduction de la résistance de béton selon la température est fournie dans le fichier fic_DTU.cfc.
- Coefficient de réduction de la résistance de l'acier
Le coefficient de réduction de la résistance de l'acier est présenté sous forme tabulaire (section 3.13 DTU P 92-701).
Une description du comportement de la résistance de l'acier selon la température est fournie dans le fichier fiy_DTU_1_2.cfy.
Dans les cas où les types d'acier 3 et 4 sont utilisés, définissez le fichier fiy_DTU_3_4.cfy, au lieu d'une valeur par défaut.
- Paramètres de calcul
Coefficients de rayonnement :
Φ*εm*εf = 0,85 de même que pour le coefficient (section 4 DTU P 92-701)
Les coefficients ci-dessus doivent être interprétés comme suit :
Φ - Coefficient de configuration
εm - Coefficient d'émission de l'élément
εf - Coefficient d'émission du feu
Coefficient de convection :
α = 6,9 [W/m2*K] = 6,0 [kcal/m2*h*oC] (section 4 DTU P 92-701)
Suppositions adoptées pour la norme EN 1992-1-2
- Développement d'incendie dans le temps en fonction de la norme EN 1991-1-2
Incendie décrit sous une forme tabulaire discrète selon la formule suivante :
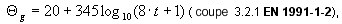
où :
t est exprimé en [min]
en supposant que la température initiale est de 20 [ 0C]
ce qui permet de décrire la température de l'incendie comme suit :
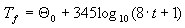. Les valeurs discrètes sont sélectionnées de sorte qu'aucun incrément de température supérieur à 30 % ne puisse s'effectuer dans aucun des incréments temporels. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du développement de l'incendie dans le temps est incluse dans le fichier Fire_EC2_N.t.
Dans le cas où d'autres types d'incendies sont employés, définissez ce qui suit au lieu d'utiliser le fichier par défaut :
feu extérieur (section 3.2.2 EN 1991-1-2): Fire_EC2_E.t
feu d'hydrocarbures (section 3.2.3 EN 1991-1-2): Fire_EC2_H.t
- Conductivité thermique du béton
La dépendance de la conductivité thermique est présentée sous forme tabulaire (section 3.4 EN 1992-1-2) - sur la base de la valeur inférieure de la conductivité thermique. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du comportement de la conductivité thermique en fonction de la température est fournie dans le fichier Lambda_EC2_L.la.
Dans le cas où la valeur supérieure est employée, définissez ce qui suit au lieu d'utiliser le fichier par défaut :
Lambda_EC2_U.la
- Poids volumique du béton
La dépendance du poids volumique est présentée sous forme tabulaire (section 3.3.2(3) EN 1992-1-2). L'interpolation linéaire est effectuée entre ces valeurs.
Une description du comportement du poids volumique selon la température est fournie dans le fichier Ro_EC2.cp.
- Chaleur spécifique du béton
La dépendance de la chaleur spécifique est présentée sous forme tabulaire (sections 3.3.2(1) and 3.3.2(2) EN 1992-1-2) sur la base de valeurs d'humidité à 1.5 %. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du comportement de la chaleur spécifique selon la température est fournie dans le fichier Cp_EC2_m015.cp.
Dans le cas où d'autres valeurs d'humidité de béton sont employées, définissez ce qui suit au lieu d'utiliser le fichier par défaut :
% de l'humidité: Cp_EC2_m000.cp
3 % d'humidité : Cp_EC2_m030.cp
- Coefficient de réduction de la résistance du béton
La dépendance du coefficient de réduction de la résistance du béton est présentée sous forme tabulaire (coupe 4.2.4.2 en 1992-1-2) sur la base de valeurs de béton avec granulats de silice. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du comportement de la réduction de la résistance de béton selon la température est fournie dans le fichier fic_EC2_Si.cfc.
Dans le cas où du béton avec granulat calcaire est employé, définissez ce qui suit au lieu d'utiliser le fichier par défaut : fic_EC2_Ca.cfc.
- Coefficient de réduction de la résistance de l'acier
La dépendance du coefficient de réduction de la résistance de l'acier est présentée sous forme tabulaire (section 3.2.3 EN 1992-1-2) sur la base de valeurs d'acier de nuance N laminé à chaud. L'interpolation linéaire est effectuée entre ces valeurs.
Une description du comportement de la réduction de la résistance de l'acier selon la température est fournie dans le fichier fiy_EC2_Nhr.cfy.
Dans le cas où d'autres types sont employés, définissez ce qui suit au lieu d'utiliser le fichier par défaut :
Acier nuance N laminé à froid : fiy_EC2_Ncw.cfy
Acier nuance X : fiy_EC2_X.cfy
- Paramètres de calcul
Coefficients de rayonnement :
Φ = 1,0 - Coefficient de configuration (section 3.1(6) EN 1991-1-2)
ε m = 0,8 - Coefficient d'émission de l'élément (section 3.1(6) EN 1991-1-2)
ε f = 1,0 - Coefficient d'émission du feu (section 3.1(6) EN 1991-1-2)
Coefficient de convection :
α ce = 25 [W/m2*K] sur le côté exposé au feu (section 3.2.1 EN 1991-1-2)
α cu = 9,0 [kcal/m2*h*oC] sur le côté non exposé au feu (section 3.1(5) EN 1991-1-2)
Calcul de la résistance de la norme BAEL - Poteaux en compression axiale
Données nécessaires aux calculs :
f cj - Résistance du béton transférée automatiquement à partir du module de poteaux BA Robot.
Φ b - Coefficient de béton selon la température Φ b (τ) (dans ce cas, τ est une température moyenne à l'intérieur de la section)
f e - Résistance de l'acier transférée automatiquement à partir du module de poteaux BA Robot.
φ si - Coefficient de l'acier selon la température φ s(τ) (dans ce cas, τ est une température de la barre i-th)
l – Hauteur du poteau
N - Charge maximale au poteau
α - Coefficient transféré automatiquement à partir du module de poteaux BA
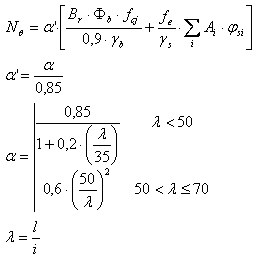
B r = A c - 0,01*u c
Br - Aire de section réduite
A c - Aire de section
u c - Périmètre de la section
γ b - Coefficient de béton 1,3
γ s - Coefficient d'acier 1,0
A i - Surface de la barre d'armature nième
Résistance du poteau :
N/NQ > 1,0