Tassement moyen

L’option de tassement moyen est disponible pour toutes les normes, excepté les normes françaises (DTU 13.12 et Fascicule 62 Titre V). L’activation de l’analyse de cet état et la définition de la valeur limite des tassements se fait dans la boîte de dialogue Options géotechnique.

Les calculs des tassements moyens bases sur les principes et les formules de la théorie d’élasticité linéaire. En particulier, ces calculs sont basés sur les contraintes calculées à partir de la formule de Boussinesque et sur le principe de superposition.

1. Le sol au-dessous de la semelle est divisé en couches dont l’épaisseur n’est pas supérieure à :
   • la moitié de la dimension plus petite de la semelle
   • 0,5 mètre
   • l’épaisseur de la couche du sol
2. Chaque couche n est analysée à partir des valeurs calculées sur la profondeur étant le centre de la couche Zn
3. Pour la profondeur Zn, la contrainte moyenne due aux charges externes, au poids de la semelle et aux terres sus-jacentes s(z) au-dessous de la semelle est définie d’après la formule suivante :
   

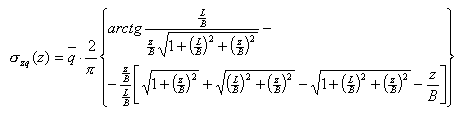
   où :

   B - dimension transversale du rectangle (semelle)

   L - dimension longitudinale du rectangle (semelle)

   Attention : une autre méthode de calcul est utilisée pour la norme SNiP 2.02.01-83 (voir les descriptions détaillées pour les normes spécifiques).

   La formule ci-dessus décrit la valeur moyenne des contraintes au-dessous de la couche rectangulaire. Elle provient de la formule de Boussinesque qui décrit la répartition des contraintes dans le demi-espace élastique dues à la charge par force concentrée.

   

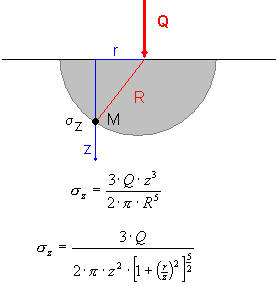
   En vous servant du principe de superposition, vous pouvez calculer la contrainte dans le point P(0,0,z) due à une couche quelconque sollicitée par la charge uniforme, conformément au principe suivant :

   

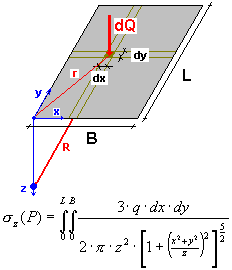
   Les solutions de l’équation ci-dessus pour les points de coin de la zone rectangulaire, au-dessus de la surface rectangulaire et la valeur moyenne au-dessous de la zone rectangulaire sont données dans la littérature. Pour obtenir la valeur de la contrainte moyenne au-dessous de la zone rectangulaire, il faut utiliser la formule présentée ci-dessous, qui après intégration, prend la forme utilisée dans l’algorithme de calcul.

   
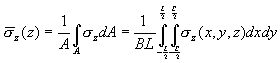
4. Pour la profondeur Zn on définit la contrainte primaire provenant des terres situées au-dessous de la couche analysée :
   

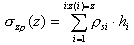
   Attention : dans le cas où les eaux phréatiques sont présentes, la poussée d’Archimède de l’eau et son poids sont pris en compte dans les calculs.

5. Les contraintes additionnelles dans le sol prises en compte dans les calculs représentent la différence des contraintes dues à la charge externe et des contraintes primaires.

   
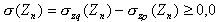
6. A partir de la caractéristique du sol, on calcule le tassement moyen de la couche n :
   

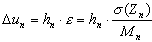
   où :

   M_0n – module primaire (sans prise en compte des effets de détente) endométrique (obtenu dans l’appareil d'effort triaxial) de compressibilité du sol dans la n-ième couche. La relation entre le module de Young et le module endométrique de compressibilité est exprimée par la formule :

   .

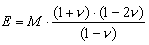   Attention : une autre méthode de calcul est utilisée pour la norme SNiP 2.02.01-83 (voir les descriptions détaillées pour les normes spécifiques).

   ATTENTION : Si la valeur du module de Poisson est absente pour le type de sol donné, les bases de sols disponibles dans le logiciel Robot pour un pays donné peuvent contenir les valeurs E = M, ce qui correspond au matériau à compressibilité idéale (ν = 0.0) ; les valeurs types du module de Poisson sont égales à 0.2¸0.3 pour les sols incohérents (la valeur 0.2 concerne les sols à gros grain, comme graves, par contre 0.3 - les sols à grain fin, comme poudres) et 0.25¸0.37 pour les sols cohérents (la valeur 0.25 concerne les sols consolidés, par contre 0.37 - les sols limoneux).

7. La compression totale du sol est la somme des compressions des couches successives.
   
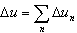
8. La sommation des couches est effectuée jusqu’à l’obtention de contraintes additionnelles de valeurs faibles adéquates (par rapport aux contraintes d’origine).

Pour les normes nationales, les exigences et les limitations suivantes sont appliquées :

1. ACI\ BS 8004:1986 \ CSA La sommation des tassements est effectuée jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 30 %.
2. DTU 13.12 \ et Fascicule 62 Titre V

   Le calcul de cet état limite n’est pas disponible.

3. ENV 1997-1:1994 (EC 7)

   Les calculs présentés dans la description générale répondent aux exigences préconisées par le point 6.6.1 et l’Annexe D. , la sommation des tassements est effectuée jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 20% [6.6.1] (2).

4. EN 1997-1:2004 (EC 7)

   Les calculs présentés dans la description générale répondent aux exigences préconisées par le point 6.6.1 et l’Annexe D. , la sommation des tassements est effectuée jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 20 % [6.6.2] (6).

5. PN-81/B-03020

   Les calculs des tassements sont effectués conformément aux exigences réglementaires (point 3.5 et Annexe 2). Les formules pour le calcul des contraintes données dans la description générale correspondent aux formules Z2-9 relatives à la contrainte moyenne au-dessous de la zone rectangulaire et à la formule 16 relative à la contrainte primaire (sans prise en compte des effets de pression de filtration) et sont utilisées dans les calculs.

   A la comparaison aux autres normes, il est possible de prendre en compte les effets de décharge du sol au moyen de l’excavation conformément à 3.5.1.2 ; les effets de décharge sont calculés comme contraintes négatives dues aux charges externes égales au poids du sol supprimé. Cette option est disponible dans la boîte de dialogue Options géotechniques (onglet Général, option Temps de réalisation du bâtiment) et correspond à la détermination de la valeur réglementaire λ égale à 0,0 ou 1,0 conformément à 3.5.3. Le tassement total de la couche du sol est calculé d’après la formule.

   

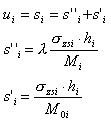
   La seconde formule est identique à la formule de calcul du tassement de la couche donnée dans l’algorithme général.

   Pour la norme polonaise, la sommation des tassements des couches est effectuée jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 30% des contraintes primaires.

6. SNiP 2.02.01-83

   Les calculs des tassements pour cette norme sont effectués conformément aux exigences réglementaires : point 2.39 et Annexe 2.

   

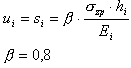
   Les contraintes dues aux charges externes sont calculées _4 partir de la formule donnée dans l’Annexe 2 (2).

   

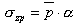
   Le coefficient α est défini à partir de l’Annexe 2 (Tableau 1) entre les valeurs du tableau qui sont interpolées de façon linéaire.

   La sommation des tassements des couches est effectuée jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 20 % des contraintes primaires, et dans le cas où pour la couche à cette profondeur le module d’Young prend la valeur E<5MPa ou la couche située directement au-dessous de celle –ci a cette valeur, les calculs sont effectués jusqu’à la profondeur à laquelle la valeur limite des contraintes additionnelles est inférieure à 10 % des contraintes (Annexe 2 point 6).