Poussée du sol - algorithmes du calcul de la poussée

Les calculs basent sur la théorie de coin de Coulomb.

Poussées du sol

Les 3 modes (limites) caractéristiques d'actions du sol (poussées) sur une construction de soutènement se différencient comme suit :

• Poussée statique Po (l’élément de soutènement ne bouge pas).
• Poussée active Pa (l’élément de soutènement bouge suite à l’action des forces extérieures dans la direction conforme à la poussée exercée par le sol).
• Poussée passive Pp (l’élément de soutènement s’est déplacé à la suite de l’action des forces extérieures dans la direction opposée à la poussée exercée par le sol).

L’état de poussée est directement lié au déplacement d’une construction de soutènement. Le déplacement est défini à l’aide du renversement de l’élément ρ, qui correspond approximativement au rapport f/H (déplacement de la crête du mur / hauteur de l’élément).

Pa <- ρ ≤ ρa

Po <- ρ = 0

Pp <- ρ ≥ ρp

Où : ρa et ρp sont les poussées limites en état approprié.

On admet que la relation entre ces poussées est une relation linéaire :

Ka * P < Ko * P < Kp * P,

Où : P, dans le cas le plus simple, est la poussée équivalent à la poussée hydrostatique. Les poussées intermédiaires apparaissent parmi les états limites de poussées.

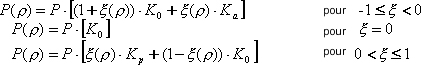
Où : ξ, de l’intervalle <-1,1>, correspond à la variable linéaire normalisée de l’intervalle <ρa, ρp>.

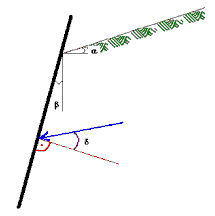
La poussée du sol dépend du poids unitaire du sol γ, de l'angle d'inclinaison naturel ϕ, de l'inclinaison d'un élément de soutènement β et de l'inclinaison du remblai α. L'effet de l'angle de frottement mur-sol δ n'est pas pris en compte.

• La poussée hydrostatique est égale au poids du sol au-dessus de la surface analysée. Pour les sols stratifiés (n couches au-dessus d’un point donné), elle est égale à :
  
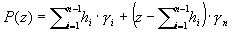
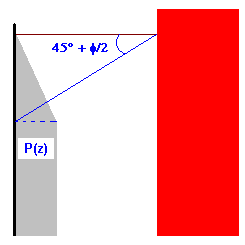
• Poussée influencée par la présence d'autres objets. Ce type de poussée se produit si, à proximité d'un élément de soutènement, d'autres objets réduisent la valeur de poussée du sol. La présence d’un tel objet provoque que la poussée P(z) ne peut pas être identifiée avec la poussée hydrostatique. La similitude avec la poussée hydrostatique est certaine jusqu’à une certaine épaisseur zép, avant de devenir constante :
  
  
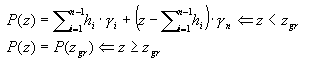
• Poussée statique : la poussée exercée par le sol quand les déplacements de l’élément de soutènement sont nuls. Cette poussée équivaut à la poussée hydrostatique multipliée par le coefficient Ko: Po(z) = Ko * P(z), où Ko = 1 - sinα.
• Poussée active : la poussée exercée par le sol dans le cas où l’élément de soutènement s’est déplacé à la suite de l’action des forces extérieures d'une valeur au moins égale à la valeur limite ra conformément à la poussée exercée par le sol. Cette poussée équivaut à la poussée hydrostatique multipliée par le facteur Ka: Pa(z) = Ka * P(z), où
  
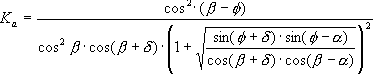
• Poussée passive : la poussée exercée par le sol dans le cas où l’élément de soutènement s’est déplacé à la suite de l’action des forces extérieures d'une valeur au moins égale à la valeur limite ρp dans le sens opposé à la poussée exercée par le sol. Cette poussée équivaut à la poussée hydrostatique multipliée par le facteur Kp: Pp(z) = Kp * P(z), où
  
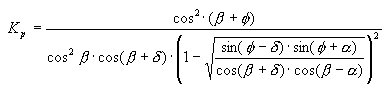
• Poussées intermédiaires : elles ont lieu quand le déplacement de l’élément de soutènement est dans l’intervalle ρa < ρ < ρp and ρ≠0. Cette poussée est une combinaison de la poussée équilibre et de la poussée active ou passive :
  

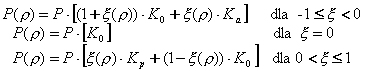
Poussées dues aux charges appliquées à la surface du sol

On admet que la poussée due aux charges appliquées au sol est obtenue par l’opération de multiplication de la poussée P'(z) par le coefficient K (Ko, Ka, Kp respectifs ou leurs combinaisons), comme pour la poussée du sol.

En fonction de la norme sélectionnée, le logiciel prend les méthodes et les coefficients de la répartition des charges ci-dessous :

Uniformes

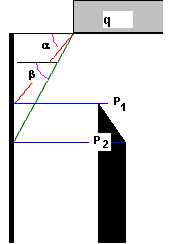
PN-83/B-03010 : α=Φ, β=45 + Φ/2 ainsi que P1= 0 et P2 =K q

PN-85/S-10030 : α=Φ, β=45 + Φ/2 ainsi que P1=K q et P2 =K q

SETRA (France) : α=Φ, β=45 + Φ/2 ainsi que P1= K q et P2 =K q

RD 31.31.27-81 (Russie) : aucun algorithme

Linéaires

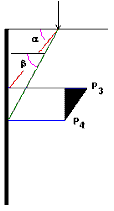
PN-83/B-03010 : α=Φ, β=45 + Φ/2 ainsi que P3= K q et P4 =0

PN-85/S-10030 : α=Φ, β=45 + Φ/2 ainsi que P3= K q et P4 =K q

SETRA (France) : α=Φ, β=45 + Φ/2 ainsi que P3= K q et P4 =K q

RD 31.31.27-81 (Russie) : α=45 + Φ/2, β=45 + Φ/2 ainsi que P3= K q et P4 =K q

Réparties

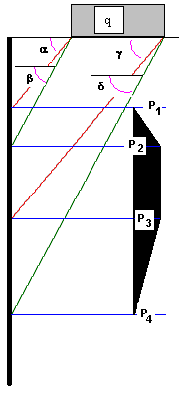
PN-83/B-03010 : α=γ=Φ, β=δ=45 + Φ/2 ainsi que P1=P4=0 et P2=P3=K q

PN-85/S-10030 : α=Φ, β=45 + Φ/2 ainsi que P1=P4= P2=P3=K q

SETRA (France) : α=Φ, β=45 + Φ/2 ainsi que P1=P4= P2=P3=K q

RD 31.31.27-81 (Russie) : α=45 + Φ/2, β=45 + Φ/2 ainsi que P1=P4= P2=P3=K q

Cohérence du sol

Les forces de cohérence du sol ne sont pas prises en compte lors de l’action de la poussée du sol. La cohérence n’est pas toujours prise en compte dans les calculs parce qu’elle agit favorablement sur la structure. C’est une force qui permet de maintenir la fouille même sans la présence de l’élément de soutènement. La cohérence agit dans la direction opposée au déplacement de l’élément de soutènement et réduit l’action du sol sur le mur. La valeur de la poussée due à la cohérence est constante pour un type de sol donné et est égale :

où c signifie la cohérence du sol, et le coefficient Kc est égale :

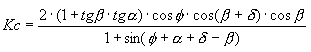
La cohérence est prise en compte uniquement pour les sols cohérents.