Vous n’êtes pas obligé de connaître le repère local de l’élément, car chaque nœud de l’élément de ce type possède son propre repère local. Mais il est important de connaître la direction du vecteur normal à la surface de l’élément fini (la même direction pour tous les éléments, si possible) car, dans le cas contraire, la définition de la charge appliquée à l’élément peut être incorrecte (par exemple la pression perpendiculaire à la surface de l’élément de type coque).
L’orientation du vecteur normal (perpendiculaire à la surface de l’élément fini) est définie conformément à la règle du boulon fileté à droite (à partir du premier vers le dernier nœud de l’élément). Les repères locaux et l’orientation du vecteur perpendiculaire à l’élément sont représentés sur la figure ci-dessous ; les éléments finis à 6 et à 8-noeuds ont été pris à titre d’exemple.
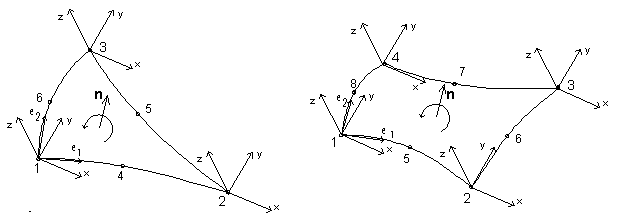
Pour les éléments finis, vous pouvez obtenir les contraintes et les efforts dans l’élément. Les grandeurs en question sont définies seulement par rapport à la direction locale normale et tangente à la section transversale. Les conventions suivantes sont utilisées pour les signes :
- n - le vecteur de la normale de la surface de la coupe de l'élément
- s - le vecteur qui est tangent à la surface de la coupe de l'élément
- z - la normale, externe à la surface des éléments.
Ces vecteurs forment un repère cartésien à règle droite. Les sens positifs des efforts, moments et contraintes agissant dans la section transversale donnée sont définis conformément à l’orientation des vecteurs n / s /z. La convention décrite ci-dessus est représentée de façon schématique sur la figure suivante. Les efforts, moments et contraintes représentés sur le dessin ont le signe positif.
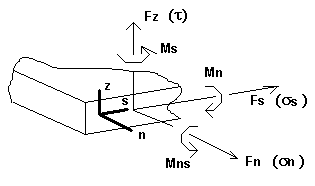
Les résultats obtenus pour les éléments finis surfaciques sont présentés dans les systèmes locaux pouvant être définis et modifiés par l’utilisateur dans chaque moment de la présentation des résultats. Par exemple, l’orientation positive des efforts et des contraintes dans le nœud est représenté sur la figure ci-dessous pour l’axe X pris comme direction de référence.
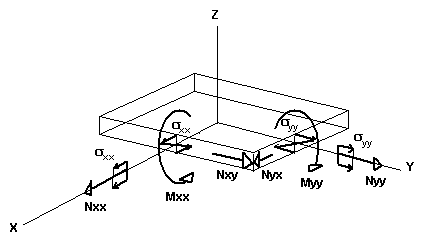
Rubrique connexe :
Numérotation des nœuds pour les éléments finis à 6 et à 8 nœuds