Analyse modale avec la prise en compte des efforts statiques - description et exemple

Les efforts statiques appliqués à la structure influent sur la fréquence des vibrations propres de la structure. L’analyse modale utilisée généralement (calcul des vibrations propres de la structure) ne prend pas en compte l’influence des efforts statiques. Pour estimer les conditions de travail réelles de la structure, l’analyse modale avec la prise en compte des efforts statiques appliqués peut être utilisée lors des calculs effectués dans le logiciel Robot.

Il existe deux formes de calcul des vibrations de structure tenant compte des forces statiques. Ces analyses sont établies par corrélation statique entre la contrainte et la déformation de l'objet sous l'influence d'une charge statique définie.

Etape 1 - Linéaire

où :

x_st - Vecteur inconnu de l'état statique

b- vecteur de la charge statique définie (vecteur de la charge statique)

K - matrice de rigidité

L (x_st, b) - Opérateur non linéaire.

Le vecteur de la charge statique peut être un cas de charge simple ou une combinaison de cas de charge définis.

Etape 2 - Analyse modale (non linéaire)

, ( 2a )

où :

K_s - Matrice de rigidité de contraintes due aux contraintes à l’état statique

M - matrice des masses

ω_i² - valeur propre (ω_i = pulsation)

Φ - Vecteur propre

Pour résoudre le problème statique non linéaire (modal), les mêmes méthodes que pour l’analyse statique non linéaire sont utilisées. Pour un problème statique linéaire, les données de corrélation contiennent : , où G est la matrice de rigidité géométrique.

Les valeurs positives ω_i (ω_i > 0) décrivent les états d'équilibre stables, tandis que les valeurs négatives (ω_i < 0) correspondent aux états d'équilibre instables. La valeur zéro (ω_i = 0) indique par conséquent l'absence de stabilité (flambement).

Si la matrice K + K_s (x_st) cesse d’être définie positivement, cela signifie que la charge statique est proche de la valeur critique (flambement). Lors de l’analyse du problème statique non linéaire, la convergence ne sera pas obtenue. Si l’approche linéaire a été sélectionnée (étape de l’analyse statique) et que la matrice n'est pas définie positivement (un message approprié est affiché à l’écran), il est conseillé d’interrompre les calculs car les calculs ultérieurs n’auront pas de sens.

Remarque : Si dans la structure, des éléments de type câble ou des éléments en traction-compression sont utilisés, seule l’approche non linéaire est possible dans le logiciel.

Exemple

A titre d’exemple, considérons la structure représentée sur la figure ci-dessous. N désigne la charge statique.

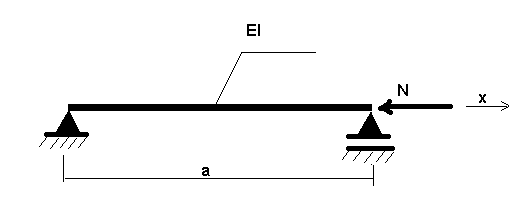
L’équation ci-dessous décrit le comportement de la structure représentée sur la figure ci-dessus.

, ( 3 )

où :

w - Déplacements dus à la flexion

ρ - Densité de la matière

F - Aire de la section transversale

La résolution de cette équation sera recherchée sous la forme suivante :

( 4 )

Après la substitution de l’expression (4) dans (3) on obtient :

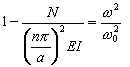, ( 5 )

où :

- charge due au flambage

ω₀² - Valeur propre pour N=0 (résultat de l’analyse modale standard).

Après transformation de cette formule finale, le résultat suivant est obtenu :

, ( 6 )

où ω² - Valeur propre obtenue pour la structure sollicitée par la charge statique N.

Le résultat de notre analyse est présenté de façon graphique sur la figure ci-dessous.

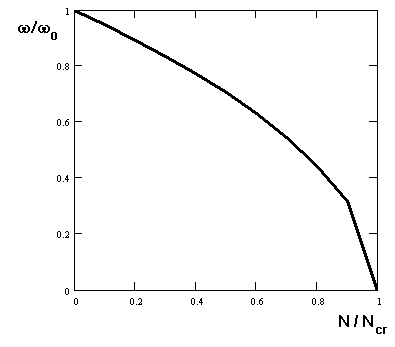
Nous pouvons conclure que pour les structures réelles, la relation ω = ω(b) est en général un peu plus complexe que celle résultant de la formule (6).