La méthode d'itération sur sous-espace par blocs permet de résoudre le problème propre généralisé.
![]() ( 1 )
( 1 )
On rencontre ce type de problème lors de l’analyse modale ou de flambement. La formule indiquée ci-dessus suppose que les symboles font référence aux objets suivants :
K - matrice de rigidité
B = M - matrice des masses dans le cas de l’analyse dynamique, pour les autres cas B = Ks
où Ks est la matrice de rigidité de contrainte due à la linéarisation de l’opérateur non-linéaire approprié dans le cas de l’analyse du flambement
λ - Valeur propre
Φ - Vecteur propre
La méthode d’itération sur sous-espace par blocs est conseillée dans les cas où, pour la structure, il faut obtenir un nombre important (souvent supérieur à 10) de couples propres (valeurs et vecteurs propres).
Si la méthode d’itération sur sous-espace par blocs est utilisée dans le logiciel, tous les types de matrices de masses peuvent être utilisés (cohérentes, concentrées avec rotations et concentrées sans rotations). Le domaine d’application de cette méthode se limite à l'analyse modale. Si vous sélectionnez la méthode de Lanczos, les deux autres modes de résolution de l’analyse modale sont disponibles (pseudomodal et sismique).
Si vous cochez la case Vérification de Sturm, le logiciel activera l’algorithme permettant de rechercher les valeurs propres ignorées dans l'analyse.
La méthode d'itérations sur sous-espace par blocs consiste en des itérations simultanées d'un vecteur dans un sous-espace avec une dimension déterminée. Chaque vecteur dont la convergence a abouti, est supprimé du sous-espace de travail et remplacé par un nouveau vecteur. L’orthogonalité de ces vecteurs est assurée pour chaque pas de l’itération. Le critère de convergence suivant est appliqué :
![]() ( 2 )
( 2 )
où :
i, k - respectivement, le numéro du mode et le numéro du pas de l’itération
tol - tolérance définie dans le champ d’édition Tolérance.
Remarquons ici que les résultats de l’analyse modale et de flambement sont calculés avec une certaine tolérance calculée suivant la formule :
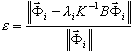 ( 3 )
( 3 )
Si la procédure de convergence est lente, il est conseillé d’utiliser la procédure de déphasage (shift) dans l’analyse modale :
![]() ( 4 )
( 4 )
où :
Kσ = K - σ M,
σ - valeur de décalage
Cliquez sur Définir paramètres pour définir les paramètres de la procédure de déphasage. Si l’option Activer le déphasage est décochée, la procédure sera activée. Le nombre d’itérations entre deux déphasages successifs est déterminant dans la procédure.
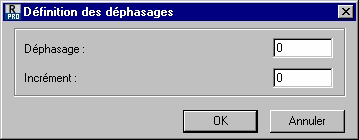
Cliquez sur Par défaut pour définir le nombre d’itérations par défaut. Si la méthode par déphasages ne peut être utilisée, décocher la case Activer le déphasage et cliquer sur le bouton OK.
La procédure par déphasages ne doit pas être utilisée pour l’analyse des problèmes de flambement car vous courez le risque d’observer la dérive des spectres des valeurs propres vers la charge critique négative, c'est-à-dire l’omission des charges critiques positives. Ceci ne se produit qu'en cas d'existence de valeurs propres négatives pour la structure.
Pour sélectionner la méthode d’itération sur sous-espace par blocs pour l’analyse du flambement de la structure, cliquez sur Changer type d’analyse dans la boîte de dialogue Type d'analyse (pour le cas de charge sélectionné) et sélectionnez l’option Flambement dans la boîte de dialogue Changement du type d’analyse. Cliquez sur OK pour accéder à la boîte de dialogue Paramètres de l’analyse de flambement et sélectionnez la méthode d’itération sur sous-espace par blocs.
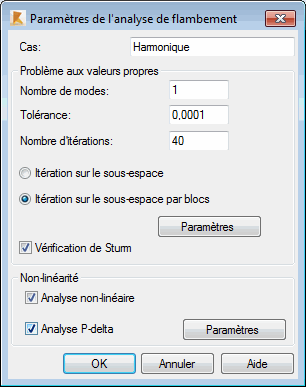
Les couples propres déterminés sont triés de la manière suivante | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n |, ce qui entraîne la définition de paramètres minimum des charges critiques dans la partie supérieure du tableau contenant les résultats.
Rubrique connexe :
Itération sur sous-espace par blocs - utilisation du déphasage