Sachez que la méthode de calcul du spectre de la réponse Sa=Sa(T) pour un diagramme des accélérations donné F(t), T étant la période, Sa étant le spectre de l'accélération, t signifie le temps et F(t) est la fonction de l'analyse temporelle donnée.
Cette option peut être fort utile si vous devez comparer les réponses sismiques obtenues en utilisant l'analyse spectrale et l'analyse temporelle. Dans ce cas, il faut affecter la courbe du spectre à la réponse Sa=Sa(T) qui se correspond précisément à la fonction de l'analyse temporelle donnée F(t) (enregistrement du diagramme des accélérations).
Cette option permet également d'effectuer l'analyse dynamique de la réponse de la structure à l'aide de la méthode de spectre de la réponse (analyse spectrale) pour le diagramme d'accélération courant. L'accélération pseudospectrale est l'accélération maximale du degré de liberté spécifique excité par le diagramme d'accélération donné :
où :
Tp - durée de l’enregistrement du séisme, ω = 2π/T - pulsation pour Tmin ≤ T ≤ Tmax, paramètre d’amortissement ξ- (exprimé en % par rapport à l’amortissement critique), F(t) - diagramme d’accélération donné.
Dans la figure 1, on admet que la fonction d'analyse temporelle F(t) est donnée. La séquence des problèmes de Cauchy (2) pour T = T1 < T2 < … < Tnpoints sera intégrée numériquement, où

Le spectre de la réponse est présenté dans la figure 2.

Figure 1
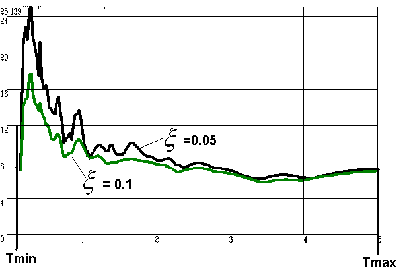
Figure 2