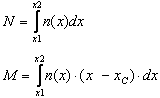Répartition des charges et calculs des contraintes dans les voiles BA

Le module de dimensionnement des voiles BA permet de définir les types des charges suivantes appliquées au voile :

• Charges uniformes - appliquées suivant la ligne horizontale sur un niveau quelconque du voile.
• Charges surfaciques - reprises à partir du plancher appuyé sur le voile, elles sont transformées aux charges uniformes appliquées au niveau quelconque du voile.
• Charges réduites - appliquées dans le plan de la base du voiles en tant que forces sectionnelles agissant dans le centre de gravité de la section inférieure du voile.

1. Charges uniformes

   Les charges uniformes et les charges surfaciques transformées en uniformes sont réparties en fonction de la distance du niveau de leur application. On a admis que si une charge a une forme libre (c’est-à-dire autre que celle uniformément répartie), à la suite de sa répartition suivant la hauteur du voile, elle est transférée en charge uniformément répartie.

   La figure ci-dessous présente le schéma de la répartition des charges gravitationnelles sur la hauteur du voile.

   

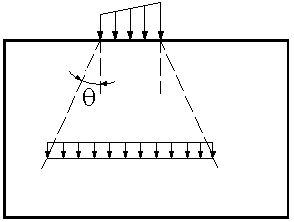
   L’angle q dépend du fait si le voile et armé ou non armé ; il est exprimé par la valeur de la fonction trigonométrique :

   • tgθ = 1/3 pour les voiles non armés
   • tgθ = 2/3 pour les voiles armés.
2. Répartition des charges reprises des linteaux des réservations

   Si dans le voile il existe des réservations, on admet que les charges supportées par le linteau sont transmises par les ‘poteaux’ adjacents aux bords de la réservation. La répartition des charges dépend de la position de la charge par rapport aux bords verticaux de la réservation. La largeur de distribution d’une charge du linteau (largeur de zones au niveau de la réservation) est considérée comme égale à la plus petite des deux valeurs : la moitié de la largeur de la réservation et le double de l’épaisseur d’un voile.

   Cette approche permet de prendre en compte la concentration des contraintes présentes par exemple dans les trumeaux.

   Le module des voiles BA facilite la définition des charges qui se répètent sur les étages successifs (supérieures au voile étudié) de la structure. Par exemple, si les charges dues au plancher appuyé sur le voile sont identiques sur tous les étages supérieurs, on peut saisir le nombre d’étages identiques au-dessus de celui étudié dans le champ Nombre d’étages au-dessus dans la boîte de dialogue de définition des charges.

   Pour une telle charge, on admet que la répartition des charges provenant des étages supérieurs sur le voile étudié est uniforme sur la longueur de la travée.

   La méthode de calcul des contraintes dues aux charges uniformes est illustrée par les formules ci-dessous :

   γ(x) = p(x) / a(x),

   où :

   γ(x) - la valeur de la contrainte dans un point x

   p(x) - la valeur de la charge répartie (forme arbitraire)

   a(x) - l’épaisseur du voile.

3. Charges réduites

   Les charges réduites sont des charges sollicitant la structure entière, si l’on considère que le bâtiment travaille comme console rigide. On a admis que les charges réduites sont appliquées à la base de l’étage donné (dans le centre de gravité de la section de la base du voile du voile avec la prise en compte des réservations). Les charges réduites peuvent être définies par l’utilisateur directement dans le module des voiles BA ou peuvent être lues (y compris la géométrie) à partir du programme Autodesk® CBS.

   La méthode de calcul des contraintes dues aux charges réduites est illustrée par les formules ci-dessous :

   • les contraintes normales au niveau de vérification i dues à l’effort réduit N

     γ(N) = N / Atot

     où :

     A_tot - aire de la section totale de la structure (y compris les réservations) sur le niveau i

   • la contrainte normale au niveau de vérification i due au moment réduit N
     

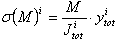
     où :

     I_tot - moment d’inertie de la section inférieure du voile (y compris les réservations) sur le niveau i

     y_tot - distance du point étudié du centre de gravité de la section de la base du voile (y compris les réservations) sur le niveau i

   • les contraintes tangentielles dues à l’effort horizontal H
     

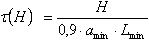
     où :

     a_min - épaisseur du voile

     L_min - longueur de la structure

4. Réduction des charges uniformes

   Si l’on applique la méthode par flexion composée d’après la norme BAEL ou l’on sélectionne la norme ACI, et aussi dans les calculs du cisaillement et du glissement dans la méthode simplifiée BAEL, les charges linéaires appliquées à un niveau quelconque du voile sont transformées au couple N-M des charges réduits dans la section de la base du voile. Les charges sont réduites d’après le schéma présenté sur la figure ci-dessous.

   

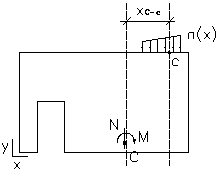
   où :