Ebben a szakaszban példákat talál olyan XML formátumokra, amelyet számos túlemelés számítási módszerhez használhat.
Példa az általános számítási módra
A következő példa bemutatja az osztatlan, tetőszelvényes utak átmeneti szelvényeinek AASHTO szabvány alapján történő számításához használható XML formátumot.
<SuperelevationAttainmentMethod name="AASHTO 2001 - Crowned Roadway">
<AttainmentStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula ="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="LCtoRC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="NStoNC" formula ="{t}*({s}-{c})/{e}">
<SuperelevationAttainmentMethod>
Ez a példa meghatároz egy „AASHTO 2001 - Crowned Roadway” (AASHTO 2001 - Tetőszelvényes útpálya) nevű számítási módszert, amely a szabványos oldalesés-átmenet túlemelés számítási módszert használja. Ez a példa tartalmaz egy, a padka eséstörés eltávolításhoz szükséges átmeneti távolság meghatározására alkalmas számítási módszert (type="NStoNC").
Példa egyoldali átmenet számítási módjára
Ebben a példában egy osztatlan, egyoldali esésű út található. A pálya nem tetőszelvényes, és nincs oldalesés-átmenet.
Az egyoldali esésű számítási módszerhez két képletre van szükség: egyre a normális keresztirányú lejtéssel szemben lévő ívekhez, egyre pedig a normális keresztirányú lejtést követő ívekhez. Az alábbi ábrán olyan normalizált sávtúlemelés látható, ahol a nem túlemelt pálya balról jobbra meg van döntve lefelé. Ezért a bal oldali ívhez hosszabb átmenetre van szükség, mint a jobb oldali ívhez.
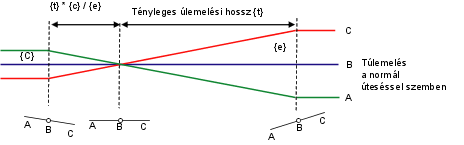
A következő példában a követő keresztszelvény határozza meg a túlemelési átmenet hosszát tartalmazó táblázatokból származó {t} értéket, azaz a normál szelvény és a teljes túlemelés közötti távolság túlemelés-átmenet hosszát 0 százalék oldaleséstől. Ebből kell kivonni a normál útpálya lejtést, azaz a {d} értéket, majd az eredményt elosztani a teljes túlemelési arány {q} értékével. A második képlet a normál szelvény és az ív kezdete közötti távolságot határozza meg {t} százalékában a {p} változó alapján, mínusz a {d} változó, osztva az {q} értékkel.
Az ellentétes keresztszelvény megadja, hogy a teljes átmeneti távolság egyezzen meg a {t} értékkel, azaz a túlemelés átmenet a 0 százalék oldaleséstől számítva. A távolság az ív kezdetéig {t} százalékos aránya a {p} változó alapján, a normál szelvény és a 0% oldalesés közötti távolság pedig a {t} * {d} / {q} képlet alapján.
<SuperelevationAttainmentMethod name="Undivided Planar Roadway">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="{t}-{t}*{c}/{e}"/>
<TransitionFormula type="NCtoBC" formula="{t}*({p}-{c}/{e})"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula="{t}*{c}/{e}"/>
</Opposing>
<SuperelevationAttainmentMethod>
Az útpálya szélessége és az átmeneti arány által meghatározott átmenetek
Nem minden cég használ olyan táblázatokat, amelyek közvetlenül adják meg a túlemelési átmenet hosszát. A következő táblázat megadja a teljes túlemelési arányt és a 
értéket a tervezési sebesség és az ívsugár függvényében. Ebben a helyzetben a érték segítségével meg lehet határozni a túlemelési átmenet hosszát az útpálya névleges szélességéből. A Túlemelési átmenet hossza táblázatban a értéket kell megadni a valós túlemelési átmenet hossza helyett.
| Sugár (m) | 90 km/h | 100km/h | 110km/h | 120km/h | ||||
|---|---|---|---|---|---|---|---|---|
| E% |
|
E% |
|
E% |
|
E% | n/a | |
| 7000 | NSZ | n/a | NSZ | n/a | NSZ | n/a | NSZ | n/a |
| 5000 | NSZ | n/a | NSZ | n/a | NSZ | n/a | 2.0 | 0.31 |
| 3000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.3 | 0.32 |
| 1500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.2 | 0.33 | 3.0 | 0.33 |
| 1400 | 2.0 | 0.39 | 2.0 | 0.34 | 2.4 | 0.33 | 3.2 | 0.34 |
| 1300 | 2.0 | 0.39 | 2.0 | 0.34 | 2.6 | 0.33 | 3.5 | 0.34 |
| 1200 | 2.0 | 0.39 | 2.2 | 0.35 | 2.8 | 0.34 | 3.8 | 0.35 |
| 1000 | 2.0 | 0.39 | 2.6 | 0.36 | 3.7 | 0.35 | 4.5 | 0.37 |
| 900 | 2.2 | 0.40 | 2.9 | 0.37 | 3.7 | 0.36 | 5.0 | 0.38 |
| 800 | 2.5 | 0.40 | 3.3 | 0.38 | 4.2 | 0.38 | 5.7 | 0.39 |
| 700 | 2.9 | 0.41 | 3.7 | 0.39 | 4.8 | 0.39 | 6.0 | 0.40 |
| 600 | 3.4 | 0.42 | 4.4 | 0.41 | 5.6 | 0.41 | ||
| 500 | 4.0 | 0.44 | 5.2 | 0.43 | 6.0 | 0.42 | ||
| 400 | 5.0 | 0.46 | 6.0 | 0.45 | ||||
| 300 | 6.0 | 0.48 | ||||||
A következő példa két, az előző táblázat alapján készített útpályához használt számítási módszereket és képleteket mutat be. A {v} változó a normál szelvény szélessége a forgáspont és a forgalmi sáv széle között. Ez a Túlemelés varázslóban van meghatározva.
<SuperelevationAttainmentMethod name="Unspiraled ramp">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoBC" formula="{p}*{e}*{w}/{t}"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
</Opposing>
</SuperelevationAttainmentMethod>
<SuperelevationAttainmentMethod name="Unspiraled 2 way roadway">
<TransitionStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
<SuperelevationAttainmentMethod>