適切な結晶形態プロパティ データを持つ熱可塑性結晶性樹脂を使用した結晶化解析を実行するオプションが利用可能となりました。
結晶化動力学モデリング
結晶性樹脂の流動誘起結晶化、せん断流動中と流動後の流動誘起形態学的変化を含む、結晶化動力学モデリングが熱可塑性樹脂のフロー ソルバーに導入されました。
結晶成長速度は、材料流動によって大きな影響は受けません。このため、成長速度は温度にのみ依存すると仮定して、Hoffman-Lauritzen 理論に従います[1]。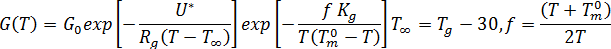 
ここで、 
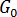と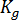 
: は、停止拘束で定義可能なグレード固有の材料係数です。 
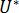は運動の活性化エネルギー、 
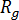はガス定数、 
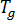はガラス転移温度、 
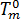は圧力のみに依存するものと仮定される材料グレード固有の平衡溶融温度です。
線形関数[2]は圧力依存性を表すために選択されています[2]。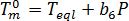 
ここで、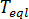 
は平衡溶融温度、 
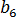はその材料の PVT モデルの材料グレード固有の定数、 P は圧力です。
核生成は、静止状態における活性化核数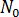 
、および流動誘起された活性化核数 
: 
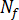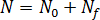
静止状態における活性化核数は、過冷却温度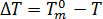 
の固有関数であると仮定し、次の式で表します[3]。 
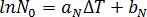ここで、 
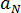、および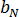 
は材料のグレード固有の定数です。
結晶化への流動の影響は、過剰自由エネルギーおよび流動誘起配向を結晶化動力学に関連付けて考慮します。流動誘起核数は、次の微分方程式で求めます。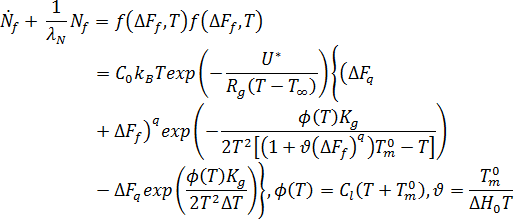 
結晶化度の進行により、粘度が増加して最終的に固化します。粘度への結晶化度の影響を表現するために、シミュレーションでは増大係数を採用しています[4]。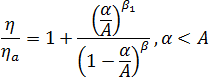 
ここで、 
は全体のシステムの粘度、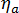 
は非晶性の粘性、 
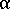は相対的な結晶化度です。
参考資料
[1] Lauritzen, S. I., and J. D. Hoffman, ''Theory of formation of polymer crystals with folded chains in dilute solution,'' J. Res. Natl. Bur. Stand. 64A, 73-102 (1960)
[2] Fulchiron, R., E. Koscher, G. Poutot, D. Delaunay, and G. Regnier, ''Analysis of the pressure effect on the crystallization kinetics: dilatometric measurements and thermal gradient modelling,'' J. Macromol. Sci., Phys. 40, 297-314 (2001)
[3] Koschei, E., and R. Fulchiron, ''Influence of shear on polypropylene crystallization: morphology development and kinetics,'' Polymer 43, 6931-6942(2002) 樹脂 43, 6931-6942 (2002)
[4] Zheng, R. and P. K. Kennedy, "A model for post-flow induced crystallization: General equations and predictions", J. Rheol., 48(4), 823-842(2004) J. Rheol., 48(4), 823-842 (2004)