熱放射モデルは、幾何学的対称性をサポートしています。対称分割は、モデルが全体モデルを正確に何等分かしたものでなければならない。例えば、1/2対称モデルは、残りの半分で完全な装置が構成される場合に有効である。同様に、1/4対称モデルは、それが実際の装置の90度分から構成され、残りの3/4で完全な装置が構成される場合に有効です。
モデルを幾何学的対称性に沿って分割しないスリップ条件では、放射伝熱の正確な結果が得られない。有効な対称/スリップ区分の例を以下に示す。
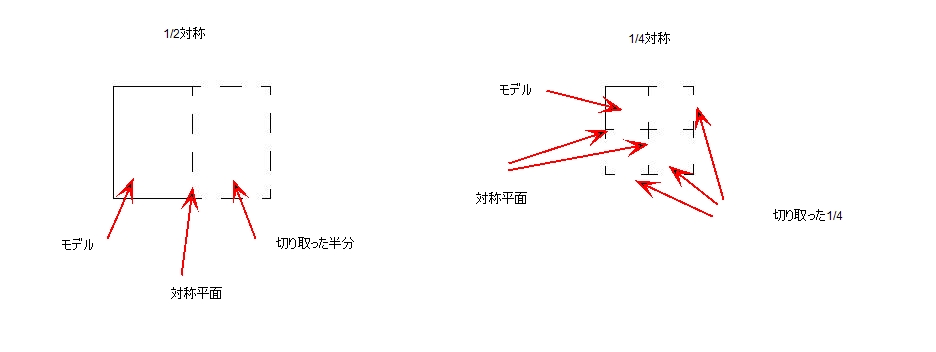
これらの2例では、有効な1/2および 1/4対称ジオメトリを示したが、有効であればさらに小さな対称モデルを使用することができる。一例として、18度のくさび形状を円盤から抜き出すことで解析することができる。これは1/20対称に相当する。重要なのは、対称性が適切に定義されるように対称(スリップ)境界条件を適用することです。
対称モデルで作業を行う場合、完全な回転対称性のモデルかどうか確認しなければならない。回転対称性と鏡面対称性の組み合わせはサポートされていません。例えば、全体ジオメトリが左側の図のように見える場合、有効な1/4対称は右側に示したようになります。
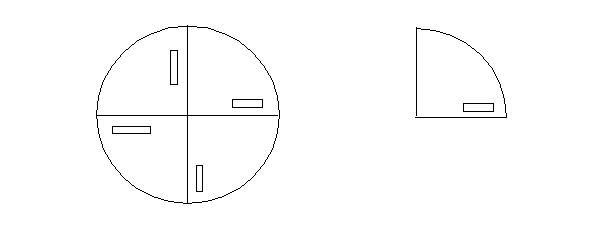
しかし、実際のジオメトリが純粋な回転対称性を持っておらず、(下記の)左側の図のように見える場合、中央の図に示した対称性は間違いである。このようなモデルで対称性を利用する正しい方法は右側の図である。
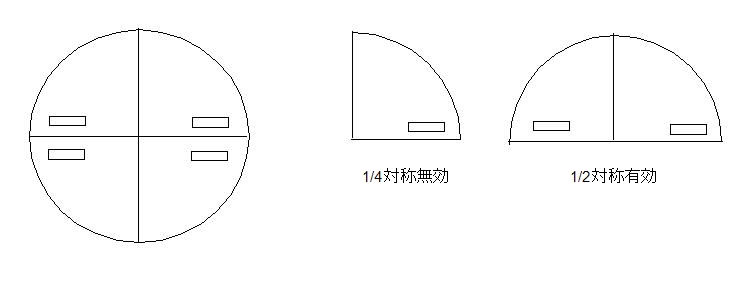
対称性を適切にモデル化するためには、対称モデルを360度回転させて元のジオメトリに戻すことができるかどうかが重要です。これは、影の発生および反射の影響が放射モデルで正確に考慮されていることを確認するためです。
熱放射モデルでは、2次元軸対称モデルもサポートされています。このようなモデルは、x軸またはy軸周りに軸対称でなければならない。
回転周期対称性も熱放射モデルでサポートされています。分割する角度は3度以上である必要があり、周期面には荷重ダイアログの周期境界条件を使用して印を付けます。しかし、並進周期対称性はサポートされていない。