回転装置または回転固体の解析は、 相対座標系(回転装置と共に回転する座標系)で流れ場を計算すると、より正確に予測を行うことができます。回転速度や回転軸が様々であり得る複数の回転装置に対応するには、各回転装置の周りに回転領域を設定することが最善です。そして、これらの回転領域は非回転領域で取り囲まれます。
下図は、各回転装置(赤)が円形の流体領域(緑)に取り囲まれている様子を示したものです。ボックスに囲まれた外側の領域は静止領域です。
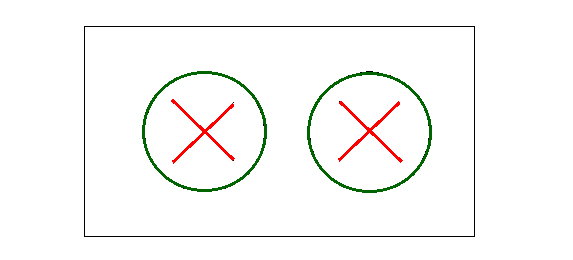
これらの流体領域は、その内部の回転装置と同じ角速度で回転します。回転領域内の計算は全て相対座標系で実行されます。静止領域内の計算は全て慣性座標系で実行されます。
流体の動きが相対座標系で計算される場合、追加の加速度が考慮されなければなりません。
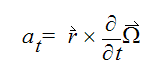
at = tangential acceleration
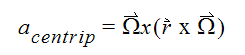
acentrip = centripital acceleration
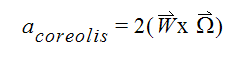
acoreolis = coreolis acceleration
ここで、慣性座標系における速度は、以下の式を用いて相対座標系における速度と関係付けられます。
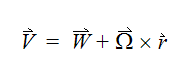
これらの追加の運動量の加速度ソース項は、回転する流体領域にのみ必須です。
各時間レベルにおいて、回転部品とその周りの流体のメッシュは、ある回転角度だけ回転します。ある回転速度における回転角度は、以下のように計算されます。
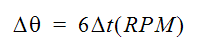
ここで、回転速度は、1分間当たりの回転数(RPM)として与えられます。新しい位置の回転メッシュによって、全てのスカラー量が、スライディングメッシュ間の回転側から非回転側に、2つのメッシュシステム間の幾何学的な補間によってマッピングされます。「移流」ベースで情報が伝達します。言い換えれば、動翼と静翼間の流束面を検討している場合、動翼から静翼への流れによって、流れの方向にスカラー量が移流されます。同様に、静翼から動翼への流れによって、静止メッシュから回転メッシュに情報が移流します。スライディングメッシュ領域を通して移動させられる運動量を結合する場合、相対座標系と絶対座標系の転換の際に「オメガクロスr」量を加減するための転換が必須であることを除き、その過程は非常に似ています。
回転装置の速度が未知である場合、角運動量の保存則が角速度の予測に利用されます。
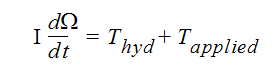
この方程式において、流体トルク(回転装置のサーフェスに作用する圧力およびせん断力から生じる)および外部から適用されるトルクは、回転装置を加速あるいは減速させます。回転装置の慣性には、Iという記号が???えられます。外部トルクの適用がない、自由回転する装置では、流体トルクが消滅するまで加速することに注意する必要があります。