流体流れおよび伝熱の支配方程式は、Navier-Stokes方程式あるいは運動量方程式、そして、熱力学の第1法則あるいはエネルギー方程式です。支配偏微分方程式は、以下のように表されます。
連続方程式:
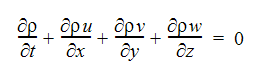
X 方向運動量方程式:
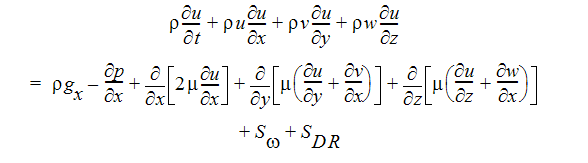
Y 方向運動量方程式:
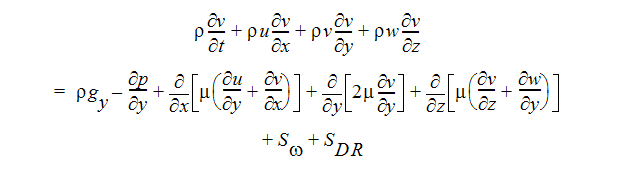
Z 方向運動量方程式:
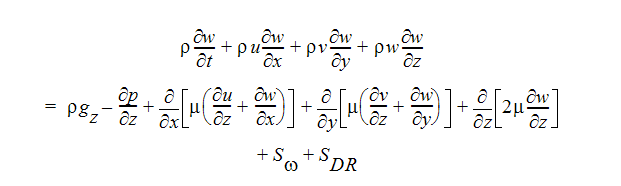
運動量方程式における2つのソース項は、それぞれ分布抵抗と回転座標に関する項です。分布抵抗項は、一般的に次のように表されます。
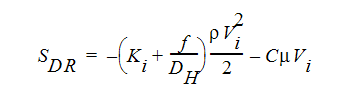
ここで、iはグローバル座標方向（u、v、w運動量方程式）を示す。 他項については前述の通りです。それぞれの方向が固有の抵抗係数Kを持つため、抵抗係数Kは1方向の運動量方程式ごとに別個に取り扱うことができます。他の2つの抵抗についても同様です。
その他のソース項は、 回転に関する項です。一般的に次のように表されます。
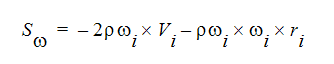
ここで、iはグローバル座標方向、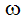
は回転速度、rは回転軸からの距離です。
非圧縮性および亜音速圧縮性流れに対するエネルギー方程式は、静温度を用いて表すことができます。
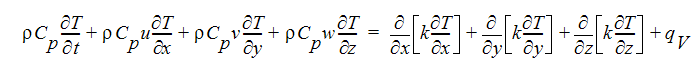
複数の相(水蒸気と水など)が混在する流れに対しては、エネルギー方程式はエンタルピーを用いて表します。
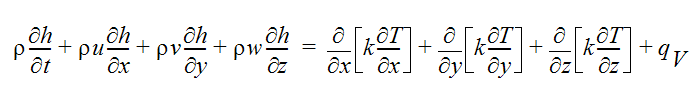
CFdesign V9.0より前のバージョンでは、 湿度の計算はエンタルピーで定式化した式を使用していました。この場合、流体の エンタルピーは、 水分(蒸気または 液体の状態)のエネルギーと、空気または搬送ガスのエネルギーの両方を表します。しかし以降のバージョンでは、相変化を表現できる比熱の取り扱いを含む温度に基づく定式化を使用しています。
水の複数の相が混在する流れについては、エンタルピーは蒸気と液体の両方の相のエネルギーになります。
圧縮性流れに対するエネルギー方程式は、 全温度を用いて表すことができます。
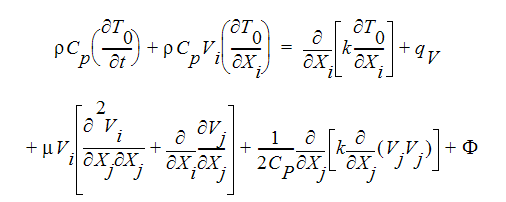
ここで、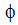 
は散逸関数です。簡便のため、全エネルギー方程式の表記には、アインシュタインテンソルを使用します。最後の3項は、圧縮性流れに対してのみ与えられます。
この方程式における変数の定義を下表に示します。
| 熱伝導率が温度に依存して変化する。 | 解説 |
| Cp | 定圧比熱 |
| gx, gy, gz | X、Y、Z方向の重力加速度 |
| h | エンタルピー |
| k | 熱伝導率 |
| p | 圧力 |
| qV | 体積発熱源 |
| T | 温度 |
| t | 時間 |
| u | 速度のX方向成分 |
| v | 速度のY方向成分 |
| w | 速度のZ方向成分 |
|
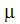
粘性係数 |
|
密度 <:so>みつど |
連続方程式・運動量方程式・エネルギー方程式は、5つの未知数（u・v・w・p・T・T o ）について5つの方程式を表します。直交座標系ジオメトリに関して、定常状態の流体流れと伝熱を記述します。
旋回速度成分（平面外成分）を持つ、軸対称ジオメトリおよび定常状態の条件に関して、方程式は以下のように表されます。
連続方程式:
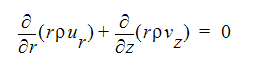
R 方向運動量方程式:
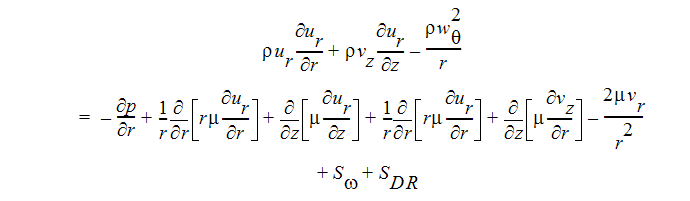
Z 方向運動量方程式:
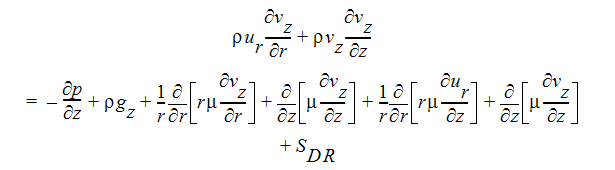
旋回流速方程式:
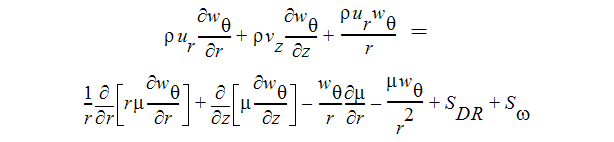
軸対称流れについて、エネルギー方程式は付加的な項を持ちません。