一般的なスカラー輸送方程式

以下の方程式は、非圧縮性流れのパッシブスカラー量の輸送を表します。

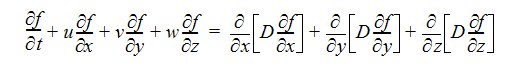
この方程式における変数の定義を下表に示します。

変数	説明
D	拡散係数 (length2/sec)
f	受動スカラー量
t	時間 (sec)
u	X方向の速度成分(length/sec)
v	Y方向の速度成分(length/sec)
w	Z方向の速度成分(length/sec)

Autodesk Simulation CFD では、種の拡散係数 (D)は[実行] > [アドバンスト] ダイアログで入力します。拡散係数の単位は、長さの２乗を時間で除算したものです （例：m2/sec）。

乱流に関して、スカラー変数を平均値と変動値（平均値に関する変動値）の重ね合わせとして表現できると仮定し、上記の方程式が時間平均化されます。例えば、スカラー変数は以下のように表すことができます。

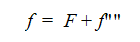
ここで、F はスカラー平均値 f"" はこの平均値に関する変動値です。これは、支配方程式に代入され、その後、方程式が平均されます。平均値を大文字で表記し、変動値を小文字で表記すると、平均された乱流スカラー方程式は、以下のように表すことができます。

平均化の処理により、スカラー方程式において uf、vf、wf の項が生成されていることに注意してください。これらの項は、非線形慣性項あるいは移流項の平均化によって生じた変動量の組合せです。

ここで、これらの付加的な項を「モデル化する」手段、すなわち付加項をもともとの未知数（平均値）に関連付け直す手段を見つける必要があります。方程式を閉じるゼロ番目のレベルにおいて、付加的な項は、従属変数F にリンクされます。

以下のように渦拡散を定義するブシネスク近似を用いて、運動量方程式と同一レベルで方程式を閉じる必要があります。

注: これらの定義は等方性の乱流を意味します。

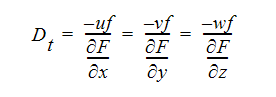
平均されたスカラー方程式においてこれらの定義が使用されると、以下のような結果となります。

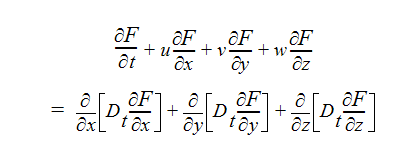
これにより、決定しなければならない変数は、渦拡散率 Dt のみとなります。

渦拡散率は、渦粘性率と乱流シュミット数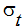を使用して計算されます。

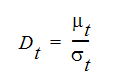
乱流シュミット数は、通常1.0とみなされます。

境界条件

スカラー方程式に条件を設定しなければならない境界には、流入口、流出口、非スリップ壁、対称面、スリップ壁、周期という6つのタイプがあります。流入口に関しては、値がゼロの場合でもスカラー値を指定しなければならなりません。流出口、対称面、スリップ／非スリップ壁において、スカラー方程式は、境界に垂直な勾配ゼロの自然境界条件を使用します。周期境界において、一方の境界のスカラー量は、他方の周期境界の対応点に適用または移行されます。

一般スカラー量による燃焼のシミュレーション

スカラー輸送方程式を使用して、燃焼を大まかにシミュレートすることができます。燃焼の速度を制限することができる過程には以下の3つがあります。

1. マクロ混合－燃料と酸化剤の大きな渦による相互作用、あるいは対流および拡散性輸送メカニズム。
2. マイクロ混合－燃料分子が酸化剤の分子に接触します。
3. 反応速度論－燃料と酸化剤が実際に反応する化学反応過程が、いくつかの中間生成物を含めた一連の化学反応によって支配されます。反応の速度は、化学種の存在割合と局所温度によって決定されます。

速度の最も遅い過程が、燃焼反応の進行に大きな影響を与えます。燃焼反応速度が1または2によって拘束される燃焼過程は、「混合限界」があると言われています。この場合、「混合されると燃焼する」と仮定することができます。混合限界のケースにおいて、燃料と酸化剤は、常に化学量論的な割合で反応して、燃焼の生成物質を形成すると仮定されます。中間種は無視されます。例えば、一般的な燃料に対して、化学量論的反応は、以下のように表すことができます。

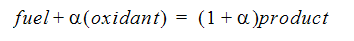
ここで、 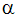は、燃料の1単位質量が燃焼するために必要な化学量論係数です。

燃料と酸化剤は、以下のように1つのスカラー変数に連結することができます。

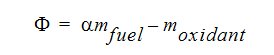
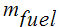• は質量分率、すなわち質量に酸化剤を可算した総質量で燃料を除した質量です。
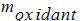• は酸化剤の質量分率です。

このスカラー変数は、保存量（すなわち定常状態の計算（ソース項・抵抗項なし）における移流および拡散の輸送バランス）となります。

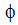の輸送方程式は均等な交換率（拡散率）を仮定して、α項に酸化剤の輸送方程式を乗じ、それを燃料種の輸送方程式から減じて導きます 。

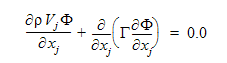
この方程式において、1番目の項は移流項、2番目の項は拡散項です。この新たに定義されたスカラー変数を用いて、以下のように混合率を定義することができます。

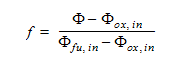
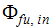• はオキシダントの流入流れのスカラー量の値です。
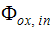• はオキシダントの流入流れのスカラー量の値です。

この混合率の定義を使用することにより、燃料の流れにおいてはf1.0、酸化剤の流れにおいては0.0となります。

化学量論的平行状態における f の値は fst とします。

f は 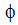の値の一次結合であり、その結果として f も保存量であることになります。したがって、fに対する輸送方程式は、以下のように表すことができます。

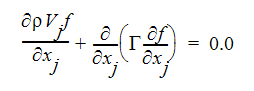
燃料と酸化剤が接触する際の平衡化学を仮定して、燃料と酸化剤の質量分率は、以下のように計算することができます。

生成物質の質量分率は、これら2つの方程式の余りから決定することができます。

注: 結果タスクで一般スカラー変数をプロットすると、f = fst のコンタ値は炎の形状と一致します。