時間とともに変化する、3次元の連続方程式、Navier-Stokes方程式、エネルギー方程式は、層流のほか、乱流にも適用されます。ただし、本質的に乱流においては、無限の時間と長さのスケールによって、例えジオメトリが単純で時間ステップが小さくても、このような方程式の計算には、膨大な数の有限要素(106～108 程度)が要求されます。実用的なアプリケーションとしては、この方法で流れをモデル化するのは非現実的です。
そのような莫大なコンピューター資源の必要性を回避するため、現在のスケールについて、支配偏微分方程式が平均されます。平均するために使用するスケールのタイプには、いくつかの選択肢があります。Autodesk Simulation CFD は、時間平均支配方程式を解きます。
時間平均方程式は、従属変数が平均値と変動値の重ね合わせとして表すことができるという仮定の基に導くことができます。例えば、x速度成分は次のように表すことができます：
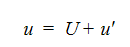
ここで、Uは平均流速、u はこの平均値に関する変動値です。これが支配方程式に代入され、支配方程式自体は、時間について平均されます。平均された支配方程式は、以下のように表されます。 平均値は大文字で、変動値は小文字で表記されています。
連続方程式
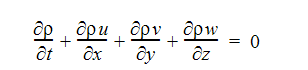
X 方向運動量方程式
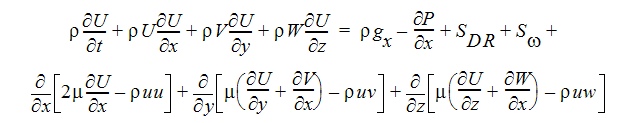
Y 方向運動量方程式
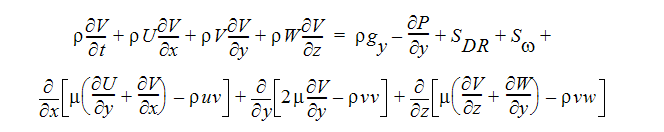
Z 方向運動量方程式
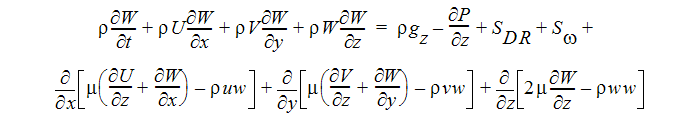
エネルギー方程式
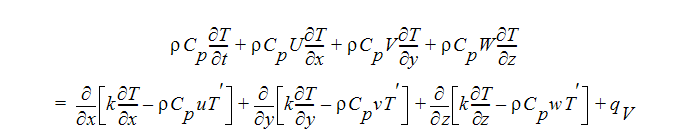
平均処理により、運動量方程式およびエネルギー方程式において、
uu、uv、uw、vv、vw、ww、CpuT'、CpvT'、CpwT' という付加的な項が生じていることに注意する必要があります。これらの項は、非線形慣性項あるいは移流項の平均化によって生じた変動量の組合せです。運動量方程式における付加的な項は、レイノルズ応力項と呼ばれます。
このような付加的な項の追加によって、上記の方程式は、uu, uv, uw, vv, vw, ww, CpuT, CpvT, CpwTという14個の未知数を、5つの方程式で表現している。上記方程式の運動量を取り上げることにより、これらの最後の追加９項の方程式を導くことができます。しかしながら、その方程式の運動量の処理により、さらに未知数が追加されることになります。この 完結問題は無限に続くことになります。ある時点で、方程式（および新規の項）の作成を終了し、付加的な項を「モデル化する」手段、すなわち項を以前の未知数に関連付け直す手段を見出す必要があります。完結のゼロ番目のレベルにおいて、レイノルズ応力項は、従属変数U・V・W・Tの平均値に関連付けられます。
一般に使用されている、ゼロ番目のレベルにおける完結手段の1つは、渦粘性モデルと交換係数を定義するブシネスク近似です。
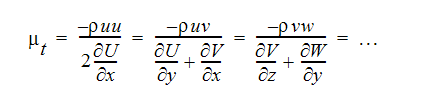
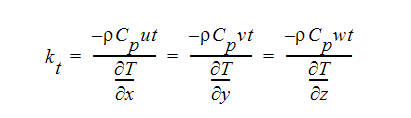
これらの定義が平均された方程式において使用されると、以下のような結果となります。
連続方程式
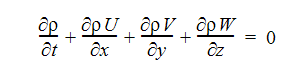
X 方向運動量方程式
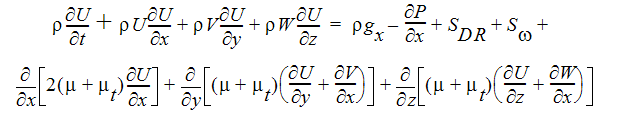
Y 方向運動量方程式
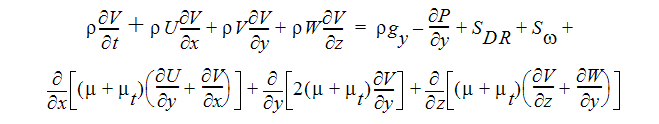
Z 方向運動量方程式
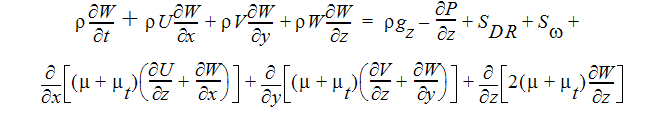
エネルギー方程式
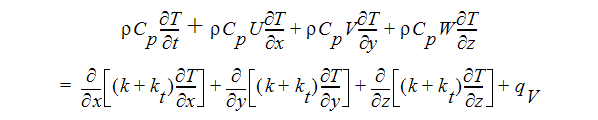
これにより、決定しなければならない変数は、渦粘性係数と交換係数のみとなります。