このページでは、どのようにして一次膜応力(Pm)と一次曲げ応力(Pb)が計算されるのかについて説明します。
これらの応力の計算には複数のステップがあります。最初に、SCL に沿った 6 つの応力テンソル σN、σT、σH、τNT、τTH、τNH を積分して、総荷重(FN、FT、FH、FNT、FTH、FHN)を求めます。次の方程式を使用します。

ここで、T は SCL に沿った位置です。
次に、6 つの成分すべての膜応力(F/A)を計算します。長さ t の SCL の場合、次の方程式を使用します。
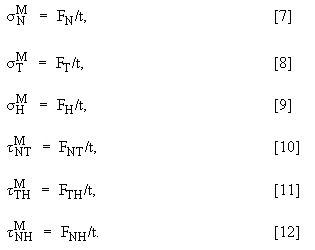
主膜応力(![]() )は、方程式 7 ~ 12 で成分が求められたテンソルにより得られます。これらの応力は、このテンソルを主軸方向で再計算することで得られます。
)は、方程式 7 ~ 12 で成分が求められたテンソルにより得られます。これらの応力は、このテンソルを主軸方向で再計算することで得られます。
次に、全応力分布から膜応力を減算して、曲げ応力を求めます。これは、応力点ごとに行います。考慮する必要があるのは、SCL に垂直な 2 つの成分応力のみです。一般的には、輪状成分応力と子午面成分応力です。最初に、長さ t の SCL のモーメント荷重分布を求めます。次に、モーメント荷重分布を積分して、断面のモーメントを求めます。

さらに、これらの積分を台形積分で計算する必要があります。後続の結果を基にして、長さ t の SCL の曲げ応力(Mc/I)を計算します。
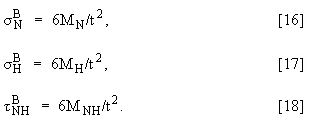
次のステップでは、SCL (![]() )の各端点の主応力を計算します。これらの主膜応力と主曲げ応力は、T = 節点 1 と T = 節点 2 を代入して成分が求められたテンソルにより得られます。
)の各端点の主応力を計算します。これらの主膜応力と主曲げ応力は、T = 節点 1 と T = 節点 2 を代入して成分が求められたテンソルにより得られます。
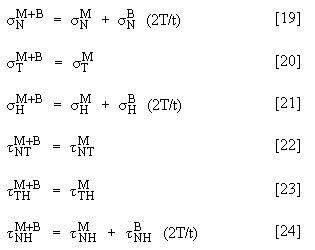
膜応力は方程式 7 ~ 12 で得られ、曲げ応力は方程式 16 ~ 18 で得られます。2 つの主応力(T = 節点 1 の主応力と T = 節点 2 の主応力)の取得方法に注意してください。また、主応力はテンソルを主軸方向で再計算することで得られます。
この時点における、取得したすべての主膜応力、
![]()
および、主膜応力と主曲げ応力の合計、
![]() 。
。
これらの値が、2 つの出力スカラー量の決定に必要です。
- Pm および
- Pm + Pb
2 つの次の式に従います:
Pm = 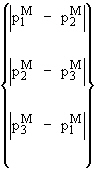 の最大値 の最大値 |
[25] |
|
Pm + Pb = |
[26] |
2 つの値セット(T = 節点 1 の値と T = 節点 2)があるため、方程式 26 は 2 回評価する必要があります。出力量は、評価で最大値となる量になります。
参考文献: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev 4, 2000.
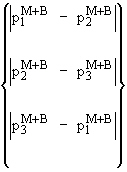 の最大値
の最大値