При расчете ортотропной плиты эквивалентная жесткость на уровне сечения рассчитывается по каждой точке. Для двумерного оболочечного элемента при расчете в 3D жесткость определяется на основе следующих матриц:
- матрица жесткости мембраны D;
- матрица жесткости при изгибе K;
- матрица жесткости при сдвиге H.
Если ортотропия определена только для двухмерных элементов и сечение симметрично, нет необходимости в определении матриц, сочетающих изгибное и безизгибное состояния.
Сечения следующих типов: двусторонние однонаправленные ребра, однонаправленный коробчатый пол, двунаправленный коробчатый пол и балочные клетки являются симметричными сечениями и для них вышеупомянутый подход полностью оправдан. Для остальных же типов конструкций такой подход может быть принят только приближенно.
Базовую плоскость для определения жесткости следует принять скорее на уровне центра тяжести, чем в на средней линии (толщина плиты). Это более правильный подход, особенно, если приходится учитывать поперечные колебания. Однако, при вычислении жесткости это тоже приближенно, но это лучше, чем принимать толщину в качестве средней линии.
Жесткость плиты определяется на основе следующих матриц:
- матрица жесткости при изгибе K;
- матрица жесткости при сдвиге H.
Эти значения жесткости (относящиеся к направлениям ортотропии) задаются матрицами, принимающими общую форму:
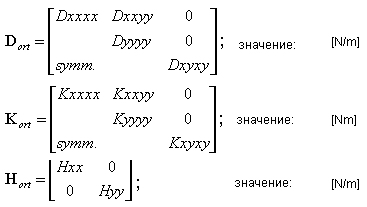
Направление ортотропии (в данном случае X) задается пользователем (определение направляющего вектора) так же, как и в случае задания локальной системы для представления результатов или армирования V = [vx,vy,vz].
Следующее правило определяет, как задаваемый пользователем вектор V, фомирует ось X системы ортотропии:
"X-направление является касательным к плоскости элемента, ближайшее к заданному направлению V".
Если {e 1 ;e 2 ;e 3 } образуют локальную базу в имеющейся точке элемента (для плит в 2D, и e i совпадает с направлениями глобальных осей XG, YG), то тригонометрические функции sin α ; cos α угла между осью ортотропии X и локальной осью x1 определяются как:
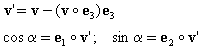
После того, как определены тригонометрические функции s = sin α ; c = cos α угла, матрицы жесткости преобразуются из системы осей ортотропии XY в локальные направления по элементу, в соответствии со следующими формулами:
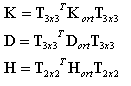
где:
T3x3 - является матрицей преобразования для тензора второго порядка в 2D (представленного в виде матрицы 3х3)
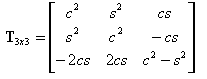
T2x2 - это матрица, представляющая преобразование 2D вектора
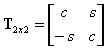
См. также: