Процедура для узловых сил
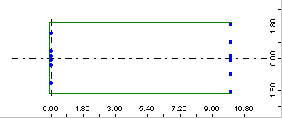
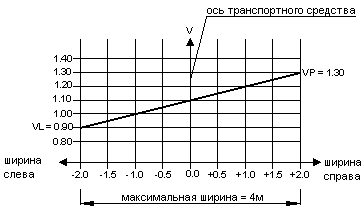
Если в предыдущем примере задать следующие значения коэффициентов: VP=1.3 и VL=0.9, то нагрузка изменится так, как показано на рисунке
- Для сил N 1, 2 и 3
Транспортное средство
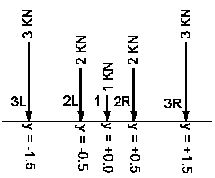
=>
Система сил
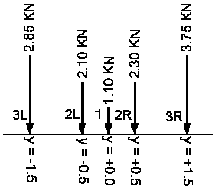
- Для сил N 4, 5 и 6
Транспортное средство
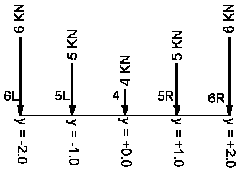
=>
Система сил
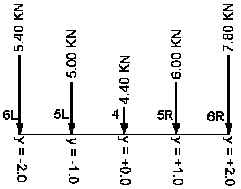
Для получения этих значений необходимо найти величину максимальной ширины нагрузки и затем умножить нагрузки, соответствующие максимальной ширине, на найденные значения коэффициентов. Если нагрузка приложена на участке, ширина которого меньше максимальной ширины нагрузки, Robot определит значение коэффициента с помощью интерполяции между значениями коэффициентов VL и VP.
Максимальная ширина = max ( S i )
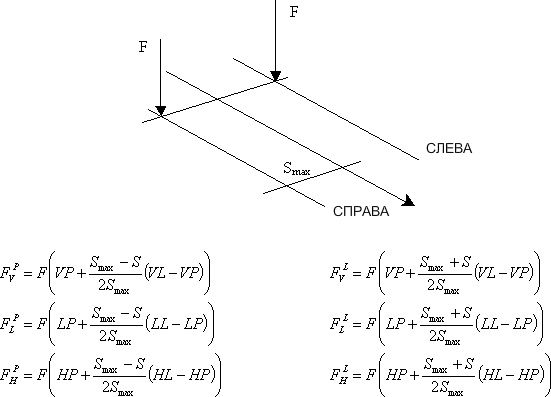
При учете коэффициентов маршрута VP,VL, HP, HL, LP, LL
Процедура для нагрузок на линиях
Процедура для линейных нагрузок аналогична процедуре для узловых сил.
Процедура для поверхностных нагрузок
В Robot предусмотрена возможность преобразования равномерной поверхностной нагрузки в трапецеидальную поверхностную нагрузку (поверхностную нагрузку, определяемую по трем точкам).
Процедура для поверхностных нагрузок аналогична процедуре для узловых и нагрузок на линиях за исключением того, что максимальная ширина нагрузки, используемая при интерполяции, должна вычисляться с учетом значений параметров S и DY.
Максимальная ширина = max ( S i + DY i )
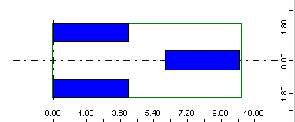
Были определены следующие значения коэффициентов: VP=1.3 и VL=0.9; во всех примерах максимальная ширина = max ( 3+1; 0+1) = 4 м.
Разложение функции представлено на рисунке внизу.
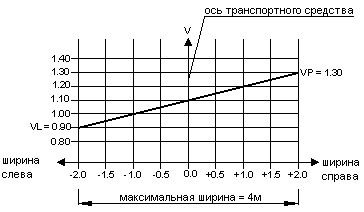
Robot изменяет нагрузку.
- Для силы N 1
Транспортное средство
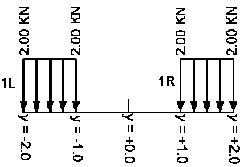
=>
Система сил
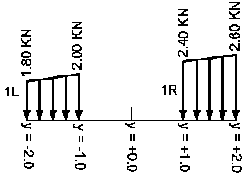
- Для силы N 2
Транспортное средство
=>
Система сил
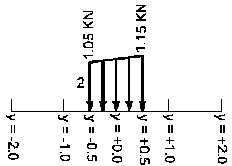
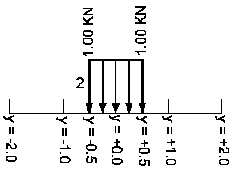
Распределение нагрузки на элементах поверхности
Линейные, плоские, сосредоточенные нагрузки трансформируются к соответствующим эквивалентным нагрузкам на конечных элементах: линейная на две точки 2D (для балок), линейная на две точки 3D (для оболочек), нагрузка на контуре, сила в точке.