Расчет качества треугольников (элементов сетки)
При создании сетки конечных элементов следует стремиться задавать такую сетку, чтобы ее элементы (возникающие треугольники) были равносторонними треугольниками. Иные треугольники, особенно тупоугольные, являются "плохими" элементами сетки с точки зрения метода конечных элементов (МКЭ).
Предполагая, что коэффициент качества треугольного элемента сетки может изменяться в промежутке <0,1> , мы примем коэффициент a равным 1 для равностороннего треугольника.
Рассчитываем коэффициент α для треугольника с вершинами ABC по следующей формуле:
Этот алгоритм основан на вычислении векторного произведения двух векторов в пространстве.
Вычисление качества четырехугольника (сетки элементов)
Подобно тому, как идеальный треугольник - равносторонний, идеальным четырехугольником является прямоугольник. При вычислении коэффициента α для четырехугольника используется метод вычисления этого коэффициента, показанный выше для треугольника.
Любой четырехугольник ABCD делим на 4 перекрывающихся треугольника ABC, ACD, ABD, BCD. Расчет коэффициентов α выполняется для определенных треугольников: {α1, a2, α3, α4} = {α (ABC), α (ACD), α (ABD), α (BCD)}. Когда эти коэффициенты вычислены, вычисляется коэффициент качества для четырехугольника.
temp1 = α1 * α3;
temp2 = α2 * α4;
если ( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0.86602540000000;
α_avg = (α_rect - fabs((α1 + α2 + α3 + α4) / 4. - α_rect))/ α_rect;
если (α_avg < α) α= α_avg;
Вычисление глобального коэффициента качества сетки
Возможны два способа вычисления глобального коэффициента:
- усредняется качество всех элементов сетки (треугольников и четырехугольников):
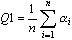
где n - число элементов сетки;
- усредняется "взвешенное" качество элементов (треугольников и четырехугольников) сетки, вес – площадь элемента сетки:
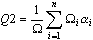
где n - количество элементов сетки, Ω - площадь.