梁单元的设计优化

假设：前端加载器的水桶由两个相同的机械系统组成。每个机械系统均承受 12 kN 的载荷（前端加载器的载荷总 24 kN），如下图所示。分析中包括实时载荷和重力。

求解：符合以下条件的初步设计：

  1. 在最大程度减少结构重量并将应力限制为 100 MPa 的情况下，三个连接（AB、BCE 和 DEFG）具有最佳横截面
  2. 圆柱 CD 和 FH 所需的尺寸。

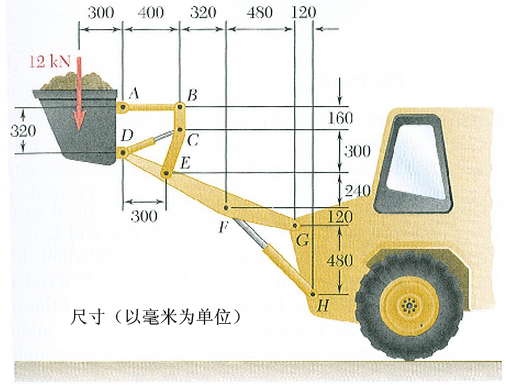
图 1

由于初步设计已完成且仅考虑平面内效果，因此横截面的形状并不十分重要。因此，我们将使用含矩形横截面的梁单元。（求解后，可根据需要代替面积和截面模量类似的不同形状。）

优化过程采用以下基本步骤执行：

您可采用以下两种方法之一，创建并输入几何体：

步骤 1 – 构建模型：

该模型将使用梁单元创建手臂（因为它们需要弯曲），使用桁架单元创建圆柱（因为它们仅传递轴向力）。初始截面如下所示：

连接 部件编号 表面编号 单元类型 初始横截面 材料
        平面外宽度 (b) x 平面内高度 (h)  
DEFG 1 2 梁 24 x 250 mm AISI 1005 钢
水桶 2 3 梁 刚性但面积较小 AISI 1005 钢
AB 3 2 梁 14 x 150 mm AISI 1005 钢
BCE 4 3 梁 20 x 150 mm AISI 1005 钢
CD 和 FH 5 任意 桁架 1900 mm2 AISI 1020 冷轧钢
表 1：FEA 属性

为了便于显示或隐藏“结果”环境中的每个连接，我们将使用不同的部件编号。为了模拟各梁之间的销轴连接，我们将在水桶（位于 A 点和 D 点处）和连接 BCE（位于 B 点和 E 点处）中使用端部释放。

模型计划如图 2 所示。由于梁单元属于三维单元，因此模型方向可以是任何方向。但是，我们按图 2 所示使用模型的 XZ 方向。（这样可让前视图变得十分自然。）根据上表，系统将显示不同的部件编号 (P)。

对于梁单元，需要先确定轴 2 的方向才能输入横截面的属性。所需的方向方案如下所示：

梁单元的方向由直线的表面数控制。表 1 和图 2 中显示的表面编号将生成所需的梁单元方向。（有关详细信息，请参见梁单元页面中的“梁单元方向”段落）。

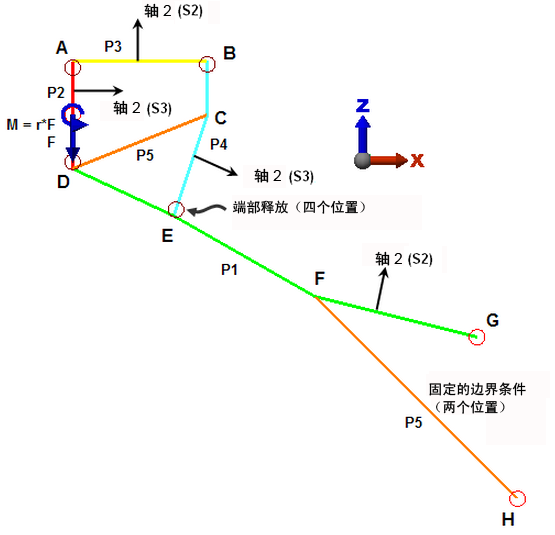
图 2：FEA 模型

图中已添加部件编号 (P)、用户确定的轴 2 方向及其指示的表面编号 (S)。

绘制几何体：

  1. 启动新的 FEA 模型（ “新建”）且
    1. 将分析类型设置为“线性: 线性材料模型静态应力”
    2. 单击“替代默认单位”按钮。

      由于尺寸以毫米为单位且载荷以牛顿为单位，因此请为模型选择牛顿、毫米和秒作为单位。

      • 将“单位制”下拉菜单设置为“自定义”。
      • 将相应的“力”、“长度”和“时间”单位分别设置为“N”、“mm”、“s”。
      • 单击“确定”按钮，以设置单位。
    3. 单击“新建”按钮并输入模型名称。
  2. 从 G 点开始绘制机械系统。使用“绘制”“绘制”“线”添加直线。
    1. 删除“用作构造”复选框中的对勾。
    2. 按图 2 所示，将“部件编号”和“表面编号”分别设置为 1 和 2。
    3. 从 (0,0,0) 开始绘制直线，然后激活“使用相对”复选框。按图 1 所示，将后面的点放在以下相对位置。（若要输入坐标，请将光标放在 X、Y 或 Z（或 DX、DY、DZ）框中，键入值并按 Enter 键。）
      点 与上一点的相对距离
      F (-480,0,120)
      E (-420,0,240)
      D (-300,0,140)
      表 2

      使“定义几何体”对话框保持打开状态。我们将创建其他直线。

  3. 此时，屏幕中的直线可能已禁用。使用“视图”“浏览”“方向”“前视图”可重新定位模型视图，并适合显示区域。
  4. 在“添加直线”对话框中，按图 2 所示，将“部件编号”和“表面编号”分别设置为 2 和 3。
    • 在相对坐标 (0,0,320) 中输入下一点 A。
  5. 按图 2 所示，将“部件编号”和“表面编号”分别设置为 3 和 2。
    • 在相对坐标 (400,0,0) 中输入下一点 B。
  6. 按图 2 所示，将“部件编号”和“表面编号”分别设置为 4 和 3。
    1. 在相对坐标 (0,0,-160) 中输入下一点 B。
    2. 使用鼠标，将连接 BCE 的最后一条线段捕捉到 E 点。（当鼠标接近 E 点时，光标将更改为挂锁，单击鼠标可将线段捕捉到该点。）
    3. 单击“X”按钮，可关闭“定义几何体”对话框。
  7. 使用“视图”“浏览”“适应窗口”，可显示整个模型。
    提示：
    • 如果绘制直线时使用的部件编号或表面编号错误，则仅需选择线段（“选择”“选择”“直线”），单击鼠标右键并选择“编辑属性”。然后设置正确的部件编号或表面编号即可。
    • 如果输入的尺寸错误，则可撤消直线（在快速访问工具栏上单击“撤消”），或选择出错的直线，将其删除并重新绘制。
  8. 梁单元应分多个线段，以获得整个构件长度的应力分布。因此，请选择所有直线（“选择”“选择”“直线”，然后“选择”“选择”“全部”）。
    1. 使用“绘制”“修改”“分割”，将选定的直线分割为 4 条单独的直线。
    2. 单击“确定”按钮执行分割操作。
  9. 使用“绘制”“绘制”“直线”，绘制表示两个圆柱的直线。
    1. 将“部件编号”更改为 5。
    2. 激活“单线”选项，这是因为两个圆柱没有连接在一起。
    3. 使用鼠标从 D 到 C 绘制一条直线。
    4. 使用鼠标，从 F 点开始绘制下一条直线。
    5. 在相对距离 (600,0,-600) 处输入最后一个点。
    6. 此时将完成几何体的绘制。因此，请单击“X”按钮以关闭“定义几何体”对话框。
  10. 如有必要，请使用“视图”“浏览”“适应窗口”，以显示整个模型。

指定 FEA 参数：

  1. 为每个部件输入名称。在浏览器（树视图）中选择“部件 <未命名>”条目，单击鼠标右键并选择“重命名”。按表 1 所示，键入每个连接的名称。
  2. 按表 1 所示，设置每个部件的单元类型。在浏览器中选择“单元类型 <未知>”条目，单击鼠标右键并选择适当的单元类型。按住 Ctrl 键并选择每个条目，然后在选定的条目之一上单击鼠标右键，即可同时设置部件 1 到 4 的单元类型。
  3. 按表 1 所示，设置每个部件的单元定义。在浏览器中选择“单元定义”条目，单击鼠标右键并选择“编辑单元定义”。对于梁单元，亮显“截面属性”电子表格中的单元格。此操作将启用“横截面库”按钮。单击该按钮后，将显示“横截面库”对话框。将左侧的“截面数据库”下拉菜单设置为“用户定义”，并将右侧的下拉菜单设置为“矩形”。根据表 1 中的尺寸和梁单元的方向，针对“h”输入高度尺寸，针对“b”输入宽度尺寸。输入尺寸之后，请单击“确定”和“确定”以设置单元定义。对于水桶（部件 2），请使用刚性部件，但采用较小的横截面面积。（优化设计时，可以明显感受到小面积的益处。）在分析中，水桶将因 12000 N 的载荷而被压缩，且因力矩而弯曲。但它不会出现任何扭转。因此，仅需在“横截面属性”电子表格中输入面积值 10 和惯性 I2 和 I3 的力矩值 100E6。将截面模量 S2 和 S3 设置为 0，以便不计算水桶的弯曲应力。（面积根据水桶部件的载荷、长度和模量进行估计，以保持合理变形，且其惯性会比其他横截面大几倍。）
  4. 按表 1 所示，设置每个部件的材料属性。在浏览器中选择“材料 <未命名>” 条目，单击鼠标右键并选择“编辑材料”。按住 Ctrl 键并选择每个条目，然后在其中某一条目上单击鼠标右键，即可同时设置部件 1 到 4 的单元类型。由于水桶的横截面面积小于其他截面，因此即便该材料包含质量密度，水桶也几乎没有重量。如果确实需要使重量为 0，则可编辑部件 2 的材料，并将质量密度设置为 0。
  5. 应用约束。选择 G 点和 H 点（“选择”“选择”“顶点”，单击 G 点，按住 Shift 键并单击 H 点）。
    1. 在显示区域中单击鼠标右键，然后选择“添加”“节点常规约束”。
    2. 单击“无平动”按钮。
    3. 单击“确定”按钮。
  6. 以上约束不会创建静态稳定的三维模型；该模型可绕 Z 轴自由转动。选择要应用载荷的顶点，单击鼠标右键并选择“添加”“节点常规约束”，可添加更多约束。
    • 激活“Ty”复选框，然后单击“确定”。此条件将防止平面外转动。
  7. 选择相同的顶点，单击鼠标右键并选择“添加”“节点力”。
    1. 针对“数值”输入 -12000。
    2. 将方向设置为“Z”。
    3. 单击“确定”按钮应用力。
  8. 选择相同的顶点，单击鼠标右键并选择“添加”“节点力矩”。
    1. 在“数值”字段中输入 -12000*300。系统将计算该乘法算式。
    2. 将方向设置为“Y”。请注意，只要单击“方向”单选按钮，系统便会对“数值”字段中的方程求值，此字段中将显示 3600000。
    3. 单击“确定”按钮以应用力矩。
  9. 将重力应用到模型。单击“设置”“载荷”“重力”。
    1. 单击“设置为标准重力”按钮，并确认方向正确无误（“Z 乘子”设置为 -1）。
    2. 转至“重力/加速度”选项卡，并将“加速度/重力”乘子设置为“1”。
  10. 默认情况下，梁单元之间的连接为刚性连接。因此，A、B、D 和 E 点中需添加端部释放，以模拟销轴条件。根据所选方向，我们知道需要释放轴 3 (R3) 的力矩，但并不知道是应先释放单元 I 端的力矩，还是 J 端的力矩。这一点可通过显示梁方向标记确定（“视图”“可见性”“对象可见性”“单元轴 1”和“单元轴 2”）。此操作向我们指出，需在 D 点和 B 点的梁端 I 处以及 A 点和 E 点的梁端 J 处释放 R3（请参见图 3）。因此
    1. 请在 D 点的水桶和 B 点的连接 BCE 选择梁单元（“选择”“选择”“线”，单击第一条直线，按住 Shift 键并单击第二条直线），
    2. 单击鼠标右键并选择“添加”梁端释放。
    3. 激活“I 节点”的“R3”复选框。
    4. 单击“确定”按钮以应用端部释放。
    5. 在 A 点和 E 点，针对多个单元重复该过程，并激活“J 节点”的“R3”复选框。
    6. 完成后，端部释放符号将显示在每个梁单元的相应端部，如图 3 所示。

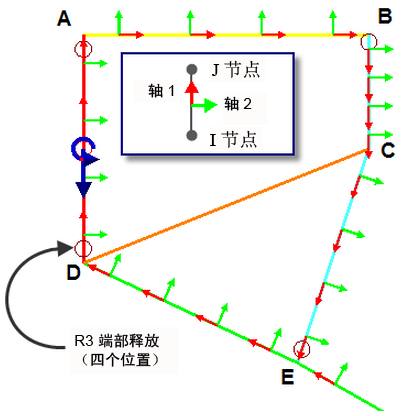
      图 3：查看梁方向以设置相应的端部释放

      每个单元中心的方向标记显示哪个方向是轴 1，从而确定哪个节点是 I，哪个节点是 J（轴 1 从节点 I 延伸至节点 J）。

  11. 您可禁用梁方向标记（“视图”“可见性”“对象可见性”“单元轴 1”和“单元轴 2”）。

步骤 2 – 运行分析：

大多数情况下，设计优化的输入取决于设置的模型结果。任何情况下最好先执行分析，确保它能够正常运行，避免执行冗长的设计优化分析。（此模型已足够小，因此事实上无需检查模型。请在执行分析后检查设置。）

  1. “分析”“分析”“运行模拟”。
  2. 完成后，模型将在“结果”环境中显示。请先检查梁方向，确认弯曲的弱轴（即设置中的轴 2）和强轴均已按预期定位。在浏览器中选择部件 1、3 和 4，单击鼠标右键并选择“三维可视化”。将显示每个单元的矩形横截面。使用“视图”“浏览”“动态观察”，四处转动模型。如果梁的定位正确，则矩形的高度应位于 XZ 平面，而较窄的宽度应位于 Y 方向。完成后，请禁用可视化。
  3. 使用“结果等值线”“位移”“位移”“数值”检查变形。可接受的变形最大值为 3 mm。
  4. 使用“结果等值线”“应力”“梁和桁架”“最差”检查应力。水桶中的人造应力将产生大量不需要的压缩应力。在浏览器中的部件 2 上单击鼠标右键，并清除“可见性”。剩余部件的应力介于 51 N/mm2 (51 MPa) 的压力和 60 N/mm2 （60 MPa) 的拉力之间。由于它限制为 100 MPa，因此还有大量的空间可用来减少横截面。
  5. 最后要确认端部释放位于正确的单元端，以便在 A、B、D 和 E 点创建销轴连接。查看弯曲强轴的力矩（“结果等值线”“其他结果”“单元受力”“轴 3 的力矩”）。若要实时检查力矩，请使用“查询结果”“探测”“探测”。当您在接近节点处按住鼠标时，该节点的结果将会显示。确认接近 A、B、D 和 E 点时的结果为 0。（在节点 E，连接 BCE 中的力矩应为 0，且连接 DEFG 应存在较大的弯曲力矩。）

步骤 3 – 指定设计变量：

由设计优化调整的参数称为“设计变量”，它们是在“单元定义”对话框中指定的。下面，我们将针对问题语句中指示的连接优化横截面的高度。

  1. 返回到 FEA 编辑器（“工具”“环境”“FEA 编辑器）。
  2. 在浏览器中，在部件 1 的“单元定义”标题上单击鼠标右键，并选择“编辑单元定义”。亮显“截面属性”电子表格中的单元格，然后单击“横截面库”按钮。在“h”字段中单击鼠标右键，并选择“设置为设计变量”。DV 符号显示矩形横截面的高度将作为设计变量。依次单击“确定”、“确定”，以保存输入。
  3. 针对部件 3 和 4，重复上述步骤。

步骤 4 – 指定设计优化参数：

  1. 使用“分析”“分析”“优化”，访问“设计优化”对话框。“设计变量”选项卡将显示模型中的设计变量集。“当前值”列使用您在“单元定义”中输入的尺寸填充。对于每个设计变量，请为“下限”输入 50；我们不希望横截面异常小。由于应力小于允许值，不必允许更大的上限，因此请输入与当前值相等的“上限”。
  2. “性能”选项卡可用来输入分析目标和所有约束。在此示例中，我们需要最大程度地减少重量（通常，这可以最大程度地降低成本）并限制应力。单击“添加行”按钮。默认情况下，此操作会添加一个最大程度地减少体积的“目标”，相当于最大程度地减少重量。（“目标”是指最大程度减少或增加的数量。）
    1. 由于只能指定一个目标行，因此要最小化的“部件”必须为“0”或“全部”。
      提示： 设计优化将调整由设计变量指定的尺寸。任何部件尺寸的减少均会减小部件体积，从而减小装配件的总体积。
    2. 若要获得“当前值”的输入，请切换回 Autodesk Simulation Mechanical 或多物理场界面，并运行“分析”“分析”“重量和重心”命令。此操作将总体积设置为 1.256e7。
      • 在“设计优化”对话框的“当前值”列中，输入 1.256e7。
      提示： 以前，指定的水桶（部件 2）横截面面积始终较小，即便我们希望水桶具有刚性亦是如此。之所以使用小面积，这是因为其体积与待优化的体积相比可能较小。如果水桶的体积相对于模型的其他部件非常大，则对部件 1、3 或 4 的体积略加更改，总体积并不会发生明显变化。我们希望避免产生这种可能会令人误解的结果。
    3. 按设计变量的下限与当前值之比来缩放每个部件的体积且合计结果，即可从“重量和重心”对话框中估计出体积的“极限值”。这将得出模型的最小总体积 4.7616E6。请将此值输入“极限值”列。
  3. 在“重量和重心”对话框中，单击“关闭”。
  4. 返回到“设计优化”对话框的“性能”选项卡中，单击“添加行”按钮三次，以添加三个新约束。我们要对每个待优化的部件设置应力上限。
    1. 将“目标/约束”更改为“最大应力”。
    2. 将“类型”设置为“上限”。
    3. 将“部件编号”分别设置为“1”、“3”和“4”。
    4. 每个部件的“当前值”均可从 Autodesk Simulation Mechanical 界面的“结果”环境中找到。（单击“结果”选项卡。）分别显示这三个部件，确定每个部件的当前应力（在浏览器中选择要隐藏的部件，单击鼠标右键并清除“可见性”）。
      • 显示某一部件的“结果等值线”“应力”“梁和桁架”“最差”结果之后，即可获得当前横截面的当前应力值。（请确保使用最大绝对值。最大应力既可是负值，也可是正值。）
      • 清除此部件的“可见性”，然后选择下一部件的“可见性”。重复操作，直到确定部件 1、3 和 4 的应力为止。
    5. 应力的最大“极限值” - 100 (MPa) 是根据问题语句设置的，而部件应力的“当前值”已在先前的步骤中确定。在相应的行和列中逐一输入这些值。正确的值已在下表 3 中列出。
      目标/约束 载荷工况 类型 部件 当前值 极限值
      体积 全部 最小化 全部 1.256E7 4.7616E6
      最大应力 全部 上限 1 59.86 100
      最大应力 全部 上限 3 5.42 100
      最大应力 全部 上限 4 27.38 100
      表 3：“性能”选项卡输入
  5. 系统将使用“参数”选项卡的默认输入并检查结果，确认它们是可接受的。

步骤 4 – 运行设计优化分析。

  1. 转至“分析”“执行设计优化”。
    • 当对话框出现之后，单击“分析”按钮以开始优化过程。
  2. 分析完成后，检查显示窗口（优化日志文件）中信息的最后几行。重要项目已在表 4 中描述。
    01 ** 对约束的更改小于限制值！
    02 ** 5 次迭代后完成优化
    03 ** 优化设计变量 **
    04 ===========================================================================
    05 设计 当前值 下限 起始值 上限
    06 ---------------------------------------------------------------------------
    07 1 1.8922e+002 5.0000e+001 2.5000e+002 2.5000e+002
    08 2 5.0000e+001 5.0000e+001 1.5000e+002 1.5000e+002
    09 3 7.6111e+001 5.0000e+001 1.5000e+002 1.5000e+002
    10 ===========================================================================
    11 ** 优化目标/约束值 **
    12 ===========================================================================
    13 对象/约束 当前值 极限值 更改/冲突
    14 ---------------------------------------------------------------------------
    15 目标 9.38600e+006 1.25600e+007 已减少 25.270701%
    16 第 1 个约束 9.96355e+001 1.00000e+002 -0.364452 % 未违反
    17 第二个约束 1.62569e+001 1.00000e+002 -83.743147 % 未违反
    18 第三个约束 9.99214e+001 1.00000e+002 -0.078580 % 未违反
    19 ===========================================================================
    20 ** 优化已完成!!**
    表 4：设计优化分析的最后一次迭代
    为了有助于以下描述，我们特别添加了行编号。
    由于不同迭代之间用户输入的约束变化小于用户输入的容差，且此优化所需的迭代次数小于输入的最大迭代次数（02 行），因此分析已收敛（01 行）。行 15 显示目标（最小化的体积）。“更改/冲突”列指示最佳设计为 25.3%，低于用户输入的当前值。第一个约束（行 16 的应力）指定上限 100 MPa。最终的最佳值为 99.6 MPa。第二个约束（行 17 的应力）远远低于上限 100 MPa。由于设计变量（行 08 的横截面高度）采用下限 50 mm，因此应力无法增加；这样一来，横截面无法再减小，应力亦不会高于 16.3 MPa。第三个约束（行 18 的应力）也限制为 100 MPa。（粗体文本亮显，与此说明对应。）
  3. 单击“完成”按钮，关闭分析窗口。由于结果可接受，因此无需更改。如果结果不可接受（如违反某一约束），则可使用约束（“设计变量”选项卡）的不同上限和下限或不同的优化参数（“参数”选项卡）重新运行设计优化。

步骤 6 – 查看最佳结果。

  1. 从“设计优化结果”菜单中，选择“设计优化历史”。稍后，“结果”框将在下拉菜单中列出每个目标、约束和设计变量。选择每个项目，查看图形，了解该值在每次迭代中如何变化。
  2. 使用“结果”菜单，并选择“最佳结果”。这将启动新的 Autodesk Simulation 实例并加载原始模型副本，但此副本的设计变量将设置为通过设计优化计算得出的最佳值。
  3. 在 Autodesk Simulation 界面中，单击“结果”选项卡，查看最佳模型结果。通过对原始模型执行一系列步骤后，我们发现位移数值 (4.5 mm) 比之前略高，但仍可接受。当然，应力结果也可接受。因此，我们将问题描述第 1 项的解答汇总在下表中。
    连接 部件编号 最佳横截面
       

    平面外宽度（“b”）

    平面内高度 x（“h”）

    DEFG 1 24 x 189 mm
    AB 3 14 x 50 mm
    BCE 4 20 x 76 mm
    表 5：最佳横截面
  4. 若要求出圆柱尺寸（问题说明的第 2 项），请隐藏除部件 5 以外的所有部件。（在浏览器中选择部件 1 到 4，右键单击其中任一部件，然后清除“可见性”。）
  5. 将结果类型设置为“结果等值线 “其他结果”“单元受力”“轴向力”。
  6. 圆柱中的力由图例或单元查询（“查询结果”“探测”“探测”）确定，如下所示。
    圆柱 轴向力
    CD 21400 N
    FH 72450 N
    表 6：圆柱力
    （4 个重要数字）

    圆柱尺寸可根据假定的流体压力计算得出。

模型的两个存档和结果均位于 Autodesk Simulation Mechanical 或多物理场安装目录的 Models 子文件夹中：

此示例基于 Beer、Ferdinand P.、Johnston、E.、Russell 共同撰写的示例 6.149 以及 McGraw Hill 所著的《Vector Mechanics for Engineers, Statics and Dynamics》，第 7 版，第 341 页。

父主题： 设计分析和优化